题目内容
(2013•房山区二模)观察下列等式:①a+
=3;②a+
=5;③a+
=7;④a+
=9…;则根据此规律第6个等式为
| 2 |
| a |
| 6 |
| a |
| 12 |
| a |
| 20 |
| a |
a+
=13
| 42 |
| a |
a+
=13
,第n个等式为| 42 |
| a |
a+
=2n+1(n为正整数).
| n(n+1) |
| a |
a+
=2n+1(n为正整数).
.| n(n+1) |
| a |
分析:观察所给的几个等式得到等式左边为a加上a的倒数的倍数,这个倍数为等式的序号数与比它大1的数的积,等式的右边为等式的序号数的2倍加1,即第n个等式为a+
=2n+1(n为正整数),然后把n=6代入可得到第6个等式.
| n(n+1) |
| a |
解答:解:第6个等式为a+
=13;
第n个等式为a+
=2n+1(n为正整数).
故答案为a+
=13;a+
=2n+1(n为正整数).
| 42 |
| a |
第n个等式为a+
| n(n+1) |
| a |
故答案为a+
| 42 |
| a |
| n(n+1) |
| a |
点评:本题考查了规律型:数字的变化类:通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
相关题目
 (2013•房山区二模)如图:⊙A、⊙B、⊙C两两不相交,且半径均为1,则图中三个阴影扇形的面积之和为( )
(2013•房山区二模)如图:⊙A、⊙B、⊙C两两不相交,且半径均为1,则图中三个阴影扇形的面积之和为( )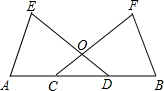 (2013•房山区二模)已知:如图,点C、D在线段AB上,E、F在AB同侧,DE与CF相交于点O,且AC=BD,AE=BF,∠A=∠B.求证:DE=CF.
(2013•房山区二模)已知:如图,点C、D在线段AB上,E、F在AB同侧,DE与CF相交于点O,且AC=BD,AE=BF,∠A=∠B.求证:DE=CF.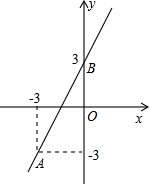 (2013•房山区二模)如图,直线AB过点A,且与y轴交于点B.
(2013•房山区二模)如图,直线AB过点A,且与y轴交于点B.