题目内容
计算题:
(1)[-0.52+(- )2-|-22-4|+(2
)2-|-22-4|+(2 )2×
)2×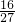 ]÷(0.1)2
]÷(0.1)2
(2)1 -2
-2 +3
+3 -4
-4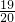 +…+(2k-1)
+…+(2k-1)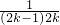 -2k
-2k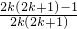 +…-2010
+…-2010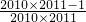
(3)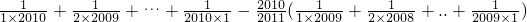 .
.
解:(1)[-0.52+(- )2-|-22-4|+(2
)2-|-22-4|+(2 )2×
)2×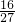 ]÷(0.1)2,
]÷(0.1)2,
=(- +
+ -|-8|+
-|-8|+ ×
×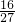 )÷
)÷ ,
,
=(-8+3)×100,
=-500;
(2)1 -2
-2 +3
+3 -4
-4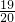 +…+(2k-1)
+…+(2k-1)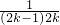 -2k
-2k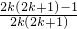 +…-2010
+…-2010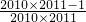 ,
,
=1+(1- )-(3-
)-(3- )+3+(
)+3+( -
- )-(5-
)-(5- )+…+(2k-1)+(
)+…+(2k-1)+( -
-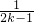 )-[2k+1-
)-[2k+1-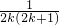 ]+…-(2010+1-
]+…-(2010+1- ),
),
=1+ -3+
-3+ -
- +3+
+3+ -
- -5+
-5+ -
- +…+(2k-1)+
+…+(2k-1)+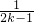 -
- -(2k+1)+
-(2k+1)+ -
-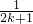 ]+…-2011+
]+…-2011+ -
- ,
,
=(1-3+3-5+5-…-2009+2009-2011)+(1- +
+ -
- +
+ -
- +
+ -
- +…+
+…+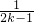 -
- +
+ -
-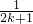 +…+
+…+ -
- ),
),
=-2010+(1- ),
),
=-2009- ,
,
=-2009 ;
;
(3)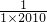 +
+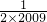 +…+
+…+ -
- (
(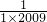 +
+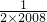 +…+
+…+ ),
),
= (1+
(1+ +
+ +
+ +…+
+…+ +1)-
+1)- ×
× (1+
(1+ +
+ +
+ +…+
+…+ +1),
+1),
= (1+
(1+ +
+ +
+ +…+
+…+ +1-1-
+1-1- -
- -
- -…-
-…- -1),
-1),
= (
( +
+ ),
),
= ×
×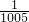 ,
,
=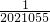 .
.
分析:(1)根据有理数的混合运算,先算乘方,然后去掉绝对值号根据运算顺序,把括号里面的计算,最后再根据除以一个数等于乘以这个数的倒数进行计算即可得解;
(2)先把带分数分离成整数与分数的形式,同时把第偶数个改写成分子是1的分数,再把分数写出两个分数的差的形式,进行计算即可得解;
(3)把前2010个分数看作被减数,后面括号里面的数看作减数,根据被减数中每一个分数的分母中两个数的和都相等,减数中每一个分数的分母中的两个数的和也都相等,可以把每一个分数写成两个分数的和的形式,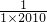 =
=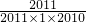 =
= (1+
(1+ ),
),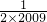 =
=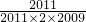 =
= (
( +
+ ),…,
),…, =
= =
= (
( +1),同理
+1),同理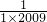 =
=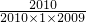 =
= (1+
(1+ ),
),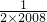 =
=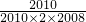 =
= (
( +
+ ),…
),… =
=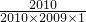 =
= (
( +1),然后根据有理数的混合运算法则以及乘法分配律进行计算即可得解.
+1),然后根据有理数的混合运算法则以及乘法分配律进行计算即可得解.
点评:本题考查了有理数的混合运算,(2)把带分数写成整数与分数的和的形式,并把分数再写出两个分数的差的形式是解题的关键,(3)根据分数的分母上的两个数的和相等,拆分成两个分数的和的形式是解题的关键,本题难度较大,规律性较强,需仔细研究,认真观察分析.
 )2-|-22-4|+(2
)2-|-22-4|+(2 )2×
)2×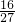 ]÷(0.1)2,
]÷(0.1)2,=(-
 +
+ -|-8|+
-|-8|+ ×
×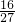 )÷
)÷ ,
,=(-8+3)×100,
=-500;
(2)1
 -2
-2 +3
+3 -4
-4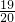 +…+(2k-1)
+…+(2k-1)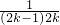 -2k
-2k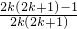 +…-2010
+…-2010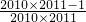 ,
,=1+(1-
 )-(3-
)-(3- )+3+(
)+3+( -
- )-(5-
)-(5- )+…+(2k-1)+(
)+…+(2k-1)+( -
-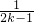 )-[2k+1-
)-[2k+1-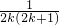 ]+…-(2010+1-
]+…-(2010+1- ),
),=1+
 -3+
-3+ -
- +3+
+3+ -
- -5+
-5+ -
- +…+(2k-1)+
+…+(2k-1)+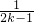 -
- -(2k+1)+
-(2k+1)+ -
-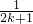 ]+…-2011+
]+…-2011+ -
- ,
,=(1-3+3-5+5-…-2009+2009-2011)+(1-
 +
+ -
- +
+ -
- +
+ -
- +…+
+…+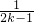 -
- +
+ -
-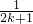 +…+
+…+ -
- ),
),=-2010+(1-
 ),
),=-2009-
 ,
,=-2009
 ;
;(3)
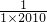 +
+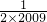 +…+
+…+ -
- (
(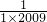 +
+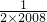 +…+
+…+ ),
),=
 (1+
(1+ +
+ +
+ +…+
+…+ +1)-
+1)- ×
× (1+
(1+ +
+ +
+ +…+
+…+ +1),
+1),=
 (1+
(1+ +
+ +
+ +…+
+…+ +1-1-
+1-1- -
- -
- -…-
-…- -1),
-1),=
 (
( +
+ ),
),=
 ×
×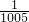 ,
,=
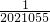 .
.分析:(1)根据有理数的混合运算,先算乘方,然后去掉绝对值号根据运算顺序,把括号里面的计算,最后再根据除以一个数等于乘以这个数的倒数进行计算即可得解;
(2)先把带分数分离成整数与分数的形式,同时把第偶数个改写成分子是1的分数,再把分数写出两个分数的差的形式,进行计算即可得解;
(3)把前2010个分数看作被减数,后面括号里面的数看作减数,根据被减数中每一个分数的分母中两个数的和都相等,减数中每一个分数的分母中的两个数的和也都相等,可以把每一个分数写成两个分数的和的形式,
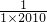 =
=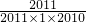 =
= (1+
(1+ ),
),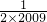 =
=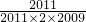 =
= (
( +
+ ),…,
),…, =
= =
= (
( +1),同理
+1),同理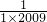 =
=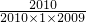 =
= (1+
(1+ ),
),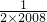 =
=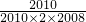 =
= (
( +
+ ),…
),… =
=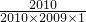 =
= (
( +1),然后根据有理数的混合运算法则以及乘法分配律进行计算即可得解.
+1),然后根据有理数的混合运算法则以及乘法分配律进行计算即可得解.点评:本题考查了有理数的混合运算,(2)把带分数写成整数与分数的和的形式,并把分数再写出两个分数的差的形式是解题的关键,(3)根据分数的分母上的两个数的和相等,拆分成两个分数的和的形式是解题的关键,本题难度较大,规律性较强,需仔细研究,认真观察分析.

练习册系列答案
相关题目
 作图计算题.
作图计算题.