题目内容
如图，在△ACD中，B为AC上一点，且∠ADB=∠C．求证：AD2=AC•AB．
分析：根据∠ADB=∠C，∠A=∠A，可推出△ADB∽△ACD，根据相似三角形的性质可得
=
，进而证出结论．
| AD |
| AC |
| AB |
| AD |
解答：证明：∵∠ADB=∠C，∠A=∠A，
∴△ADB∽△ACD，
∴
=
，
∴AD2=AC•AB．
∴△ADB∽△ACD，
∴
| AD |
| AC |
| AB |
| AD |
∴AD2=AC•AB．
点评：此题主要考查了相似三角形的判定与性质，关键是掌握相似三角形的判定方法．
练习册系列答案
阅读快车系列答案
相关题目
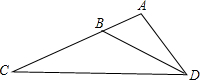如图，在△ACD中，B为AC上一点，且∠ADB=∠C，AC=4，AD=2，求：AB的长．
，
，
，
，
，
，
，
，
，