题目内容
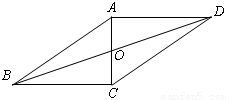
如图已知四边形ABCD的对角线AC与BD相交于O,若S△AOB=4,S△COD=9,则四边形ABCD的面积的最小值为 .
【答案】分析:先根据正弦定理及三角形的面积公式表示出△AOB及△COD的面积,再求出四边形ABCD面积的表达式,根据均值公式即可得出其最小值.
解答: 解:由题得:∵S△AOB=
解:由题得:∵S△AOB= =4,
=4,
S△COD= =9,
=9,
∴ =4,
=4,
 =9,
=9,
∴ ×
× =4×9=36,
=4×9=36,
即: =36,
=36,
∴S四边形ABCD=S△AOB+S△COD+S△AOD+S△BOC
=13+ +
+ ≥13+2
≥13+2 ×
× =13+2
=13+2 =13+2×6=25,
=13+2×6=25,
当且仅当: =
= 时取等号.
时取等号.
∴S△AOD=S△BOC=6时,
∴四边形ABCD的面积最小值为25.
故答案为:25.
点评:本题考查的是等积变换、三角形的面积公式及正弦定理,根据S△AOB=4,S△COD=9得出两三角形面积的表达式是解答此题的关键.
解答:
 解:由题得:∵S△AOB=
解:由题得:∵S△AOB= =4,
=4,S△COD=
 =9,
=9,∴
 =4,
=4, =9,
=9,∴
 ×
× =4×9=36,
=4×9=36,即:
 =36,
=36,∴S四边形ABCD=S△AOB+S△COD+S△AOD+S△BOC
=13+
 +
+ ≥13+2
≥13+2 ×
× =13+2
=13+2 =13+2×6=25,
=13+2×6=25,当且仅当:
 =
= 时取等号.
时取等号.∴S△AOD=S△BOC=6时,
∴四边形ABCD的面积最小值为25.
故答案为:25.
点评:本题考查的是等积变换、三角形的面积公式及正弦定理,根据S△AOB=4,S△COD=9得出两三角形面积的表达式是解答此题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目

 如图已知AB为⊙O的直径,弦AC∥BD,连接AD与BC.
如图已知AB为⊙O的直径,弦AC∥BD,连接AD与BC. 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD.