题目内容
阅读下列材料:
若关于x的一元二次方程ax2+bx+c=0(a≠0)的两个实数根分别为x1,x2,则x1+x2=-
,x1•x2=
.
解决下列问题:
已知:a,b,c均为非零实数,且a>b>c,关于x的一元二次方程ax2+bx+c=0有两个实数根,其中一根为2.
(1)填空:4a+2b+c
(2)利用阅读材料中的结论直接写出方程ax2+bx+c=0的另一个实数根(用含a,c的代数式表示).
若关于x的一元二次方程ax2+bx+c=0(a≠0)的两个实数根分别为x1,x2,则x1+x2=-
| b |
| a |
| c |
| a |
解决下列问题:
已知:a,b,c均为非零实数,且a>b>c,关于x的一元二次方程ax2+bx+c=0有两个实数根,其中一根为2.
(1)填空:4a+2b+c
=
=
0,a>
>
0,c<
<
0;(填“>”,“<”或“=”)(2)利用阅读材料中的结论直接写出方程ax2+bx+c=0的另一个实数根(用含a,c的代数式表示).
分析:(1)由关于x的一元二次方程ax2+bx+c=0有两个实数根,其中一根为2,根据方程解的知识,可得4a+2b+c=0,然后设方程ax2+bx+c=0的另一根为x1,由根与系数的关系可得:x1+2=-
,2x1=
,然后分别从若x1为正与若x1为负去分析求解即可求得答案;
(2)由(1):2x1=
,即可求得答案.
| b |
| a |
| c |
| a |
(2)由(1):2x1=
| c |
| a |
解答:解:(1)∵关于x的一元二次方程ax2+bx+c=0有两个实数根,其中一根为2,
∴将x=2代入ax2+bx+c=0得:4a+2b+c=0,
设方程ax2+bx+c=0的另一根为x1,
∴x1+2=-
,2x1=
,
∵a>b>c,
若x1为正,则a>0,b<0,c>0(舍去);
若x1为负,则a>0,c<0;
故答案为:=,>,<.
(2)由(1)可得:
设方程ax2+bx+c=0的另一根为x1,
∴2x1=
,
∴方程ax2+bx+c=0的另一个实数根为:
.
∴将x=2代入ax2+bx+c=0得:4a+2b+c=0,
设方程ax2+bx+c=0的另一根为x1,
∴x1+2=-
| b |
| a |
| c |
| a |
∵a>b>c,
若x1为正,则a>0,b<0,c>0(舍去);
若x1为负,则a>0,c<0;
故答案为:=,>,<.
(2)由(1)可得:
设方程ax2+bx+c=0的另一根为x1,
∴2x1=
| c |
| a |
∴方程ax2+bx+c=0的另一个实数根为:
| c |
| 2a |
点评:此题考查了根与系数的关系以及方程根的定义.此题难度适中,注意若二次项系数不为1,则常用以下关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
 的一元二次方程
的一元二次方程
 的两个实数根分别为
的两个实数根分别为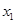 、
、 ,则
,则 ,
, 
 有两个非零不等实数根
有两个非零不等实数根 .
.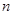 的取值范围;
的取值范围; ;
; 值,使
值,使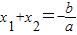 ,
, .
.