题目内容
已知在△ABC中,AB=4,AC=3,BC边上的高等于2.4,则△ABC的周长=________.
12或8.4
分析:此题分两种情况:∠C为锐角或钝角.△ABC的周长为AB+AC+BC,已知AB、AC的值,所以要求三角形的周长,只需求出BC的值即可.如下图所示:作AD⊥BC于D,则AD为BC边上的高,在Rt△ADC中,由勾股定理得:AC2=AD2+DC2,在Rt△ADB中,由勾股定理得:AB2=AD2+BD2,代入AB=4,AC=3,AD=2.4,可求出BD、DC的值,BC=BD+DC或BC=BD-DC,将AB、BC、AC的值代入周长公式,可求出该三角形的周长.
解答: 解:①当∠C为锐角:
解:①当∠C为锐角:
作AD⊥BC于D,则AD为BC边上的高,AD=2.4,如下图所示:
在Rt△ADC中,由勾股定理得:
AC2=AD2+DC2,
∴DC=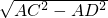 =
= =1.8,
=1.8,
在Rt△ADB中,由勾股定理得:
AB2=AD2+BD2,
∴BD=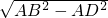 =
= =3.2,
=3.2,
∴BC=BD+DC=3.2+1.8=5,
所以,△ABC的周长为AB+AC+BC=4+3+5=12.
②当∠C为钝角:
作AD⊥BC,交BC的延长线于D,则AD为BC边上的高,AD=12,
如图所示:在Rt△ADC中,由勾股定理得:
AC2=AD2+DC2,
∴DC=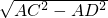 =
= =1.8,
=1.8,
在Rt△ADB中,由勾股定理得:
AB2=AD2+BD2,
∴BD=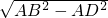 =
= =3.2,
=3.2,
∴BC=BD-DC=3.2-1.8=1.4,
所以,△ABC的周长为AB+AC+BC=4+3+1.4=8.4.
故△ABC的周长为12或8.4.
故答案为:12或8.4.
点评:本题主要考查运用勾股定理结合三角形的周长公式求三角形周长的能力,三角形的周长等于三边之和.
分析:此题分两种情况:∠C为锐角或钝角.△ABC的周长为AB+AC+BC,已知AB、AC的值,所以要求三角形的周长,只需求出BC的值即可.如下图所示:作AD⊥BC于D,则AD为BC边上的高,在Rt△ADC中,由勾股定理得:AC2=AD2+DC2,在Rt△ADB中,由勾股定理得:AB2=AD2+BD2,代入AB=4,AC=3,AD=2.4,可求出BD、DC的值,BC=BD+DC或BC=BD-DC,将AB、BC、AC的值代入周长公式,可求出该三角形的周长.
解答:
 解:①当∠C为锐角:
解:①当∠C为锐角:作AD⊥BC于D,则AD为BC边上的高,AD=2.4,如下图所示:
在Rt△ADC中,由勾股定理得:
AC2=AD2+DC2,
∴DC=
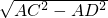 =
= =1.8,
=1.8,在Rt△ADB中,由勾股定理得:
AB2=AD2+BD2,
∴BD=
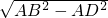 =
= =3.2,
=3.2,∴BC=BD+DC=3.2+1.8=5,
所以,△ABC的周长为AB+AC+BC=4+3+5=12.
②当∠C为钝角:

作AD⊥BC,交BC的延长线于D,则AD为BC边上的高,AD=12,
如图所示:在Rt△ADC中,由勾股定理得:
AC2=AD2+DC2,
∴DC=
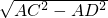 =
= =1.8,
=1.8,在Rt△ADB中,由勾股定理得:
AB2=AD2+BD2,
∴BD=
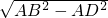 =
= =3.2,
=3.2,∴BC=BD-DC=3.2-1.8=1.4,
所以,△ABC的周长为AB+AC+BC=4+3+1.4=8.4.
故△ABC的周长为12或8.4.
故答案为:12或8.4.
点评:本题主要考查运用勾股定理结合三角形的周长公式求三角形周长的能力,三角形的周长等于三边之和.

练习册系列答案
相关题目
 22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.
22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.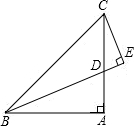 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC.
如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC. 如图,已知在△ABC中,∠B与∠C的平分线交于点P.
如图,已知在△ABC中,∠B与∠C的平分线交于点P.