Question

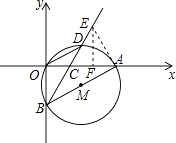
【题目】如图，在直角坐标系中，⊙M经过原点O（0，0），点A（ ，0）与点B（0，﹣ ），点D在劣弧 上，连接BD交x轴于点C，且∠COD=∠CBO．
（1）求⊙M的半径；
（2）求证：BD平分∠ABO；
（3）在线段BD的延长线上找一点E，使得直线AE恰好为⊙M的切线，求此时点E的坐标．

Answer 1

【答案】
（1）解：∵点A（ ，0）与点B（0，﹣ ），

∴OA= ，OB= ，

∴AB= =2 ，

∵∠AOB=90°，

∴AB是直径，

∴⊙M的半径为：

（2）解：∵∠COD=∠CBO，∠COD=∠CBA，

∴∠CBO=∠CBA，

即BD平分∠ABO

（3）解：如图，过点A作AE⊥AB，垂足为A，交BD的延长线于点E，过点E作EF⊥OA于点F，即AE是切线，

∵在Rt△AOB中，tan∠OAB= = = ，

∴∠OAB=30°，

∴∠ABO=90°﹣∠OAB=60°，

∴∠ABC=∠OBC= ∠ABO=30°，

∴OC=OBtan30°= × = ，

∴AC=OA﹣OC= ，

∴∠ACE=∠ABC+∠OAB=60°，

∴∠EAC=60°，

∴△ACE是等边三角形，

∴AE=AC= ，

∴AF= AE= ，EF= AE= ，

∴OF=OA﹣AF= ，

∴点E的坐标为：（ ， ）．

【解析】（1）由点A（ ，0）与点B（0，﹣ ），可求得线段AB的长，然后由∠AOB=90°，可得AB是直径，继而求得⊙M的半径；（2）由圆周角定理可得：∠COD=∠ABC，又由∠COD=∠CBO，即可得BD平分∠ABO；（3）首先过点A作AE⊥AB，垂足为A，交BD的延长线于点E，过点E作EF⊥OA于点F，易得△AEC是等边三角形，继而求得EF与AF的长，则可求得点E的坐标．