题目内容
已知x= ,求
,求 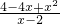 -
-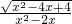 的值.
的值.
解:∵x= =
=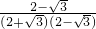 =2-
=2- ,
,
∴x-2=2- -2=-
-2=- <0,
<0,
∴|x-2|=2-x,
则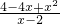 -
-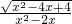
= -
-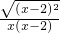
=x-2-
=x-2+
=2- -2+
-2+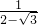
=2- -2+2+
-2+2+
=2.
分析:将x= 右边的式子分子分母同时乘以2-
右边的式子分子分母同时乘以2- ,分母利用平方差公式及二次根式的化简公式化简后,得到最简结果,求出x-2的值小于0,然后将所求式子第一项分子利用完全平方公式变形,第二项分子利用完全平方公式,二次根式的化简公式及绝对值的代数意义化简,分母提取x分解因式,约分后得到最简结果,将化简后的x的值代入计算,即可求出值.
,分母利用平方差公式及二次根式的化简公式化简后,得到最简结果,求出x-2的值小于0,然后将所求式子第一项分子利用完全平方公式变形,第二项分子利用完全平方公式,二次根式的化简公式及绝对值的代数意义化简,分母提取x分解因式,约分后得到最简结果,将化简后的x的值代入计算,即可求出值.
点评:此题考查了二次根式的化简求值,涉及的知识有:二次根式的化简,完全平方公式的运用,绝对值的代数意义,以及分母有理化,
 =
=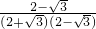 =2-
=2- ,
,∴x-2=2-
 -2=-
-2=- <0,
<0,∴|x-2|=2-x,
则
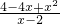 -
-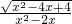
=
 -
-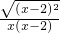
=x-2-

=x-2+

=2-
 -2+
-2+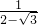
=2-
 -2+2+
-2+2+
=2.
分析:将x=
 右边的式子分子分母同时乘以2-
右边的式子分子分母同时乘以2- ,分母利用平方差公式及二次根式的化简公式化简后,得到最简结果,求出x-2的值小于0,然后将所求式子第一项分子利用完全平方公式变形,第二项分子利用完全平方公式,二次根式的化简公式及绝对值的代数意义化简,分母提取x分解因式,约分后得到最简结果,将化简后的x的值代入计算,即可求出值.
,分母利用平方差公式及二次根式的化简公式化简后,得到最简结果,求出x-2的值小于0,然后将所求式子第一项分子利用完全平方公式变形,第二项分子利用完全平方公式,二次根式的化简公式及绝对值的代数意义化简,分母提取x分解因式,约分后得到最简结果,将化简后的x的值代入计算,即可求出值.点评:此题考查了二次根式的化简求值,涉及的知识有:二次根式的化简,完全平方公式的运用,绝对值的代数意义,以及分母有理化,

练习册系列答案
相关题目
 ,
, ,求代数式
,求代数式 的值。
的值。 ,
, 求:
求: 的值.
的值. ,求分式
,求分式 的值:
的值: ,求代数式
,求代数式 的值.
的值.