题目内容
设n为整数,请你证明(2n+1)2-5一定能被4整除.
证明:∵(2n+1)2-5=4n2+4n+1-5=4n2+4n-4=4(n2+n-1)
又∵n是整数,
则4(n2+n-1)一定能被4整除.
∴(2n+1)2-5一定能被4整除.
分析:先运用完全平方公式将式子展开,合并后提取公因式4,可得4(n2+n-1),从而得证.
点评:本题考查的知识点:因式分解,倍数问题.把原式化为4(n2+n-1)是此题的关键.
又∵n是整数,
则4(n2+n-1)一定能被4整除.
∴(2n+1)2-5一定能被4整除.
分析:先运用完全平方公式将式子展开,合并后提取公因式4,可得4(n2+n-1),从而得证.
点评:本题考查的知识点:因式分解,倍数问题.把原式化为4(n2+n-1)是此题的关键.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
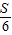 =m;第二步:
=m;第二步: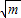 =k;第三步:分别用3、4、5乘k,得三边长”.
=k;第三步:分别用3、4、5乘k,得三边长”.