题目内容
已知点A(1,5),B(3,-1),点M在x轴上,当AM-BM最大时,点M的坐标为 .
【答案】分析:作点B关于x轴的对称点B′,连接AB′并延长与x轴的交点,即为所求的M点.利用待定系数法求出直线AB′的解析式,然后求出其与x轴交点的坐标,即M点的坐标.
解答: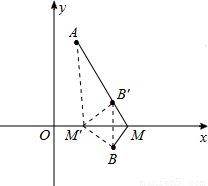 解:如图,作点B关于x轴的对称点B′,连接AB′并延长与x轴的交点,即为所求的M点.此时AM-BM=AM-B′M=AB′.
解:如图,作点B关于x轴的对称点B′,连接AB′并延长与x轴的交点,即为所求的M点.此时AM-BM=AM-B′M=AB′.
不妨在x轴上任取一个另一点M′,连接M′A、M′B、M′B′.
则M′A-M′B=M′A-M′B′<AB′(三角形两边之差小于第三边).
∴M′A-M′B<AM-BM,即此时AM-BM最大.
∵B′是B(3,-1)关于x轴的对称点,∴B′(3,1).
设直线AB′解析式为y=kx+b,把A(1,5)和B′(3,1)代入得:
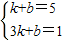 ,解得
,解得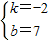 ,
,
∴直线AB′解析式为y=-2x+7.
令y=0,解得x= ,
,
∴M点坐标为( ,0).
,0).
故答案为:( ,0).
,0).
点评:本题考查了轴对称--最短路线问题、坐标与图形性质.解题时可能感觉无从下手,主要原因是平时习惯了线段之和最小的问题,突然碰到线段之差最大的问题感觉一筹莫展.其实两类问题本质上是相通的,前者是通过对称转化为“两点之间线段最短”问题,而后者(本题)是通过对称转化为“三角形两边之差小于第三边”问题.可见学习知识要活学活用,灵活变通.
解答:
 解:如图,作点B关于x轴的对称点B′,连接AB′并延长与x轴的交点,即为所求的M点.此时AM-BM=AM-B′M=AB′.
解:如图,作点B关于x轴的对称点B′,连接AB′并延长与x轴的交点,即为所求的M点.此时AM-BM=AM-B′M=AB′.不妨在x轴上任取一个另一点M′,连接M′A、M′B、M′B′.
则M′A-M′B=M′A-M′B′<AB′(三角形两边之差小于第三边).
∴M′A-M′B<AM-BM,即此时AM-BM最大.
∵B′是B(3,-1)关于x轴的对称点,∴B′(3,1).
设直线AB′解析式为y=kx+b,把A(1,5)和B′(3,1)代入得:
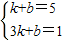 ,解得
,解得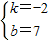 ,
,∴直线AB′解析式为y=-2x+7.
令y=0,解得x=
 ,
,∴M点坐标为(
 ,0).
,0).故答案为:(
 ,0).
,0).点评:本题考查了轴对称--最短路线问题、坐标与图形性质.解题时可能感觉无从下手,主要原因是平时习惯了线段之和最小的问题,突然碰到线段之差最大的问题感觉一筹莫展.其实两类问题本质上是相通的,前者是通过对称转化为“两点之间线段最短”问题,而后者(本题)是通过对称转化为“三角形两边之差小于第三边”问题.可见学习知识要活学活用,灵活变通.

练习册系列答案
相关题目
 14、如图,已知点A,B,C在⊙O上,AC∥OB,∠BOC=40°,则∠ABO=
14、如图,已知点A,B,C在⊙O上,AC∥OB,∠BOC=40°,则∠ABO= 2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.
2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.