题目内容
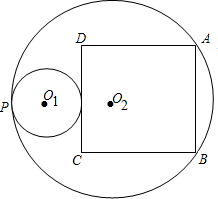（2012•蕲春县模拟）如图⊙O1与⊙O2内切于点P，正方形ABCD的顶点A、B在⊙O2上，边CD与⊙O1相切，若⊙O1的直径是3，⊙O2的半径是5，求正方形的边长．分析：在图中构造直角三角形，利用勾股定理中的相等关系作为等量关系列方程求解即可．
解答：
解：连接AO2，PO2，作O2E垂直AB于E，
∵⊙O1的直径是3，⊙O2的半径是5，设AB=a，
∴NO2=5-3=2，
∵AO2=5 O2E=a-2，AE=
，
∴52=（
）2+（a-2）2，
解得，a=6．
解：连接AO2，PO2，作O2E垂直AB于E，∵⊙O1的直径是3，⊙O2的半径是5，设AB=a，
∴NO2=5-3=2，
∵AO2=5 O2E=a-2，AE=
| a |
| 2 |
∴52=（
| a |
| 2 |
解得，a=6．
点评：本题考查了由两圆位置关系来判断半径和圆心距之间数量关系，解题关键是要知道圆心和切点的连线垂直于切线，相切两圆的性质：如果两圆相切，那么切点一定在连心线上．
练习册系列答案
相关题目
（2012•蕲春县模拟）如图，△ABC是⊙O的内接三角形，AE是直径，AD是高交⊙O于F，连接BE、CF，下列结论正确的有几个？（ ）