��Ŀ����
��ֱ������ϵxOy�У���֪��P�Ƿ���������y�� ��x��0��ͼ����һ�����㣬��PΪԲ�ĵ�Բʼ����y�����У����е�ΪA��
��x��0��ͼ����һ�����㣬��PΪԲ�ĵ�Բʼ����y�����У����е�ΪA��
��1����ͼ1����P�˶�����x�����У����е�ΪK���ж��ı���OKPA����״����˵�����ɣ�
��2����ͼ2����P�˶�����x���ཻ���轻��ΪB��C�����ı���ABCP������ʱ��
�������A��B��C�����꣮
���ڹ�A��B��C��������������Ƿ���ڵ�M��ʹ��MBP�����������ABCP����� �������ڣ��������������������M������ꣻ�������ڣ���˵�����ɣ�
�������ڣ��������������������M������ꣻ�������ڣ���˵�����ɣ�

��1���ı���OKPA�������Σ�
֤�����ߡ�P�ֱ��������������У�
��PA��OA��PK��OK��
 ���PAO=��OKP=90�㣮
���PAO=��OKP=90�㣮
�֡ߡ�AOK=90�㣬
���PAO=��OKP=��AOK=90�㣮
���ı���OKPA�Ǿ��Σ�
�֡�AP=KP��
���ı���OKPA�������Σ�
��2��������PB������P��PG��BC��G��
���ı���ABCPΪ���Σ�
��BC=PA=PB=PC���뾶����
���PBCΪ�ȱ������Σ���Rt��PBG�У���PBG=60�㣬PB=PA=x��PG=
��P�� ������
������
��֮�ã�x=��2����ֵ��ȥ����
��PG= ��PA=BC=2��P(2,
��PA=BC=2��P(2,  )
)
��֪�ı���OGPA�Ǿ��Σ�PA=OG=2��BG=CG=1��
��OB=OG-BG=1��OC=OG+GC=3��
��A��0�� ����B��1��0����C��3��0����
����B��1��0����C��3��0����
������κ�������ʽΪ�� ������A��0��
������A��0�� ����
����
�� ����κ�������ʽΪ��y��
����κ�������ʽΪ��y�� x2−
x2− x+
x+ 

��ֱ��BP�Ľ���ʽΪ��y=ux+v��������ã� ��֮�ã�
��֮�ã� ��
��
��ֱ��BP�Ľ���ʽΪ��y=  x-
x- ��
��
Ҫʹ
����A��ֱ��AM��BP����ɵ�ֱ��AM�Ľ���ʽΪ��y�� x+
x+ ��
��
�ⷽ���飺
�ã� ��
�� ��
��
����C��ֱ��CM��PB�������ֱ��CM�Ľ���ʽΪ��y�� x+t��
x+t��
��0=3 +t��
+t��
��t��−3 ��
��
��ֱ��CM�Ľ���ʽΪ��y�� x−3
x−3 ��
��
�ⷽ���飺
�ã� ��
�� ����
����
���Ͽ�֪������������M���������ĸ���
�ֱ�Ϊ����0�� ������3��0������4��
������3��0������4�� ������7��8
������7��8 ��
��

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д���ͼ����֪��A��D��C��F��ͬһ��ֱ���ϣ�AB=DE��BC=EF��Ҫʹ
��ABC �ա�DEF������Ҫ����һ�������ǣ� ��.
| A����B=��E | B����BCA=��F |
| C��BC // EF | D����A=��EDF |
|
|
 =3
=3 ��
�� =3
=3 +
+ D.
D. =-7
=-7 ��ͼ,▱ABCD�ĶԽ���AC,BD�ཻ�ڵ�O,��E,F�ֱ����߶�AO,BO���е�.��AC+BD=24����,��OAB���ܳ���18����,��EF=������������.
��ͼ,▱ABCD�ĶԽ���AC,BD�ཻ�ڵ�O,��E,F�ֱ����߶�AO,BO���е�.��AC+BD=24����,��OAB���ܳ���18����,��EF=������������.
 ��������6�֣�
��������6�֣�
 ��ʵ����Χ�������壬��
��ʵ����Χ�������壬��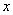 ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� �� ��
��

