题目内容
如图,△ABC是等腰直角三角形,过点A,点B作AD⊥BD,且AD=3BD,设BD=x,△BCD的面积为y,则y与x函数关系式是 .
【答案】分析:过C点作CF⊥AD于E点,根据等腰直角三角形的性质得到∠BAC=90°,AB=AC,利用等角的余角相等得∠BAD=∠ACE,又AB=CA,∠ADB=∠AEC=90°,根据全等三角形的判定得△ABD≌△CAE,利用全等三角形的性质有BD=AE,AD=CE,又AD=3BD,BD=x,则AD=CE=3x,根据勾股定理可计算出AB= x,而y=S△CBD=S△ABD+S△ADC-S△ABC,然后根据三角形的面积公式进行计算即可得到y与x函数关系式.
x,而y=S△CBD=S△ABD+S△ADC-S△ABC,然后根据三角形的面积公式进行计算即可得到y与x函数关系式.
解答:解:过C点作CF⊥AD于E点,如图,
∴∠AEC=90°,
∵△ABC是等腰直角三角形,
∴∠BAC=90°,AB=AC,
∴∠BAD=∠ACE,
在△ABD和△CAE中

∴△ABD≌△CAE,
∴BD=AE,AD=CE,
∵AD=3BD,设BD=x,
∴AD=CE=3x,AB= =
= =
= x,
x,
∴y=S△CBD
=S△ABD+S△ADC-S△ABC
= •3x•x+
•3x•x+ •3x•3x-
•3x•3x- •(
•( x)2
x)2
=x2.
故答案为y=x2.
点评:本题考查了全等三角形的判定与性质:有两组对应角相等,并且有一条边对应相等的两个三角形全等;全等三角形的对应边相等.也考查了等腰直角三角形的性质以及三角形的面积公式.
 x,而y=S△CBD=S△ABD+S△ADC-S△ABC,然后根据三角形的面积公式进行计算即可得到y与x函数关系式.
x,而y=S△CBD=S△ABD+S△ADC-S△ABC,然后根据三角形的面积公式进行计算即可得到y与x函数关系式.解答:解:过C点作CF⊥AD于E点,如图,

∴∠AEC=90°,
∵△ABC是等腰直角三角形,
∴∠BAC=90°,AB=AC,
∴∠BAD=∠ACE,
在△ABD和△CAE中

∴△ABD≌△CAE,
∴BD=AE,AD=CE,
∵AD=3BD,设BD=x,
∴AD=CE=3x,AB=
 =
= =
= x,
x,∴y=S△CBD
=S△ABD+S△ADC-S△ABC
=
 •3x•x+
•3x•x+ •3x•3x-
•3x•3x- •(
•( x)2
x)2=x2.
故答案为y=x2.
点评:本题考查了全等三角形的判定与性质:有两组对应角相等,并且有一条边对应相等的两个三角形全等;全等三角形的对应边相等.也考查了等腰直角三角形的性质以及三角形的面积公式.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一定点,延长BP至P′,将△ABP绕点A旋转后,与△ACP′重合,如果AP=
如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一定点,延长BP至P′,将△ABP绕点A旋转后,与△ACP′重合,如果AP=
 如图,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是
如图,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是 (2012•资阳)如图,△ABC是等腰三角形,点D是底边BC上异于BC中点的一个点,∠ADE=∠DAC,DE=AC.运用这个图(不添加辅助线)可以说明下列哪一个命题是假命题?( )
(2012•资阳)如图,△ABC是等腰三角形,点D是底边BC上异于BC中点的一个点,∠ADE=∠DAC,DE=AC.运用这个图(不添加辅助线)可以说明下列哪一个命题是假命题?( )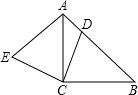 已知:如图,△ABC是等腰直角三角形,D为斜边AB上任意一点(不与A,B重合),连接CD,作EC⊥DC,且EC=DC,连接AE.
已知:如图,△ABC是等腰直角三角形,D为斜边AB上任意一点(不与A,B重合),连接CD,作EC⊥DC,且EC=DC,连接AE.