题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]()
![]() 与
与![]() 轴、
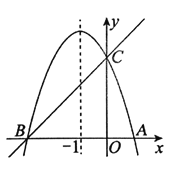
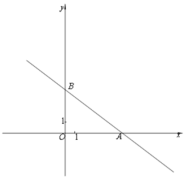
轴、![]() 轴分别交于点A、B如图所示,点
轴分别交于点A、B如图所示,点![]() 在线段
在线段![]() 的延长线上,且
的延长线上,且![]() .
.
(1)用含字母![]() 的代数式表示点
的代数式表示点![]() 的坐标;
的坐标;
(2)抛物线y经过点![]() 、
、![]() ,求此抛物线的表达式;
,求此抛物线的表达式;
(3)在第(2)题的条件下,位于第四象限的抛物线上,是否存在这样的点![]() :使
:使![]() ,如果存在,求出点
,如果存在,求出点![]() 的坐标,如果不存在,试说明理由.
的坐标,如果不存在,试说明理由.
【答案】(1) C![]() ; (2)
; (2) ![]() ; (3)见解析.
; (3)见解析.
【解析】
(1)求出点A、B的坐标分别为![]() ,利用
,利用
![]() ,即可求解;
,即可求解;
(2)将点A、C坐标代入函数表达式,联立方程组,解得m、b的值,即可求解;
(3)![]() 即可求解.
即可求解.
解:
(1) 过点![]() 作
作![]() ⊥
⊥![]() ,垂足为点
,垂足为点![]() .
.
∵直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() 、
、![]() ,
,
∴点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() .
.
∴![]() ,
,![]() .
.
∵![]() ⊥
⊥![]() ,∴
,∴![]() //
//![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∴点![]() 的坐标是
的坐标是![]() .
.
(2) ∵抛物线![]() 经过点
经过点![]() 、点
、点![]() ,可得
,可得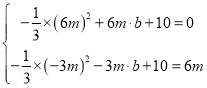
∵![]() ,解得
,解得 ![]() .
.
∴抛物线的表达式是![]() .
.
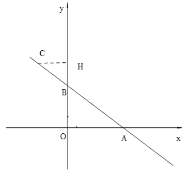
(3)过点![]() 分别作
分别作![]() ⊥
⊥![]() 、垂足为点
、垂足为点![]() .
.
设点![]() 的坐标为
的坐标为![]() .可得
.可得![]() ,
,![]() .
.
∵![]() ,
,![]() .
.
∴△![]() 与△
与△![]() 等高,∴
等高,∴![]() //
//![]() .
.
∴![]() .∴
.∴![]() .
.
∴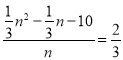 .
.
解得 ![]() ,
,![]() (舍去).
(舍去).
∴点![]() 的坐标是
的坐标是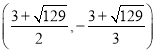 .
.

练习册系列答案
相关题目