题目内容
顺次连接任意四边形四条边中点，所得的四边形是（ ）A．菱形
B．矩形
C．平行四边形
D．正方形
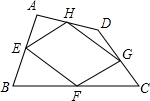
【答案】分析：首先根据题意作出图形，由点E，F，G，H分别是四边形ABCD边AD，AB，BC，CD的中点，根据三角形中位线的性质，易得EF∥BD∥GH，EF=GH=
BD，继而可证得四边形EFGH是平行四边形．
解答：
解：如图，点E，F，G，H分别是四边形ABCD边AD，AB，BC，CD的中点．
连接BD，
∵点E，F，G，H分别是四边形ABCD边AD，AB，BC，CD的中点，
∴EF∥BD，EF=
BD，GH∥BD，GH=
BD，
∴EF∥GH，EF=GH，
∴四边形EFGH是平行四边形．
故选C．
点评：此题考查了中点四边形，平行四边形的性质以及三角形中位线的性质．此题难度不大，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
BD，继而可证得四边形EFGH是平行四边形．解答：
解：如图，点E，F，G，H分别是四边形ABCD边AD，AB，BC，CD的中点．连接BD，
∵点E，F，G，H分别是四边形ABCD边AD，AB，BC，CD的中点，
∴EF∥BD，EF=
BD，GH∥BD，GH=BD，∴EF∥GH，EF=GH，
∴四边形EFGH是平行四边形．
故选C．
点评：此题考查了中点四边形，平行四边形的性质以及三角形中位线的性质．此题难度不大，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
通城学典默写能手系列答案
相关题目
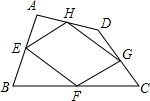顺次连接任意四边形ABCD各边中点，所得的四边形EFGH是中点四边形．下列四个叙述：①中点四边形EFGH一定是平行四边形；②当四边形ABCD是矩形时，中点四边形EFGH也是矩形；③当中点四边形EFGH是菱形时，四边形ABCD是矩形；④当四边形ABCD是正方形时，中点四边形EFGH也是正方形．其中正确的是
顺次连接任意四边形ABCD各边中点，所得的四边形EFGH是中点四边形．下列四个叙述：①中点四边形EFGH一定是平行四边形；②当四边形ABCD是矩形时，中点四边形EFGH也是矩形；③当中点四边形EFGH是菱形时，四边形ABCD是矩形；④当四边形ABCD是正方形时，中点四边形EFGH也是正方形．其中正确的是________（只填代号）．