Question

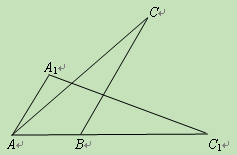
如图，将一个钝角△ABC（其中∠ABC=120°）绕点B顺时针旋转得△A₁BC₁，使得C点落在AB的延长线上的点C₁处，连接AA₁．
（1）写出旋转角的度数；
（2）求证：∠A₁AC=∠C₁．

Answer 1

（1）解：∵∠ABC=120°，
∴∠CBC₁=180°-∠ABC=180°-120°=60°，
∴旋转角为60°；

（2）证明：由题意可知：△ABC≌△A₁BC₁，
∴A₁B=AB，∠C=∠C₁，
由（1）知，∠ABA₁=60°，
∴△A₁AB是等边三角形，
∴∠BAA₁=60°，
∴∠BAA₁=∠CBC₁，
∴AA₁∥BC，
∴∠A₁AC=∠C，
∴∠A₁AC=∠C₁．
分析：（1）∠CBC₁即为旋转角，其中∠ABC=120°，所以，∠CBC₁=180°-∠ABC；
（2）由题意知，△ABC≌△A₁BC₁，易证△A₁AB是等边三角形，得到AA₁∥BC，继而得出结论；
点评：本题考查了旋转的性质、全等三角形的判定和性质及等边三角形的判定和性质，熟练掌握这些性质是解答本题的关键．