Question

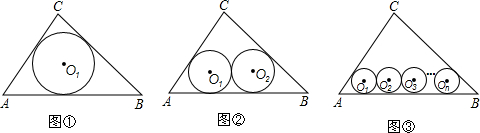
已知Rt△ABC中，∠ACB=90°，AC=6，BC=8．
（Ⅰ）如图①，若半径为r₁的⊙O₁是Rt△ABC的内切圆，求r₁；
（Ⅱ）如图②，若半径为r₂的两个等圆⊙O₁、⊙O₂外切，且⊙O₁与AC、AB相切，⊙O₂与BC、AB相切，求r₂；
（Ⅲ）如图③，当n大于2的正整数时，若半径r_n的n个等圆⊙O₁、⊙O₂、…、⊙O_n依次外切，且⊙O₁与AC、BC相切，⊙O_n与BC、AB相切，⊙O₁、⊙O₂、⊙O₃、…、⊙O_n-1均与AB边相切，求r_n．

Answer 1

分析：（I）连接三角形的内心和三角形的各个顶点，根据三角形的总面积等于分割成的三个小三角形的面积，进行计算；
（II）连接两圆的圆心和每个圆的圆心和三角形的三个顶点，把大三角形分割成了三个三角形和一个梯形，根据三角形的总面积等于四部分的面积的和，进行计算；
（III）连接第一个圆和最后一个圆的圆心，以及两个圆的圆心和三角形的三个顶点，根据（II）的思路进行计算．

解答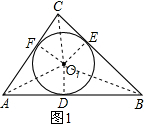：解：（I）∵在Rt△ABC中，∠ACB=90°，AC=6，BC=8，
∴AB=

AC2+BC2

=10．
如图1，设⊙O₁与Rt△ABC的边AB，BC，CA分别切于点D，E，F．
连接O₁D，O₁E，O₁F，AO₁，BO₁，CO₁．
于是O₁D⊥AB，O₁E⊥BC，O₁F⊥AC．
S△AO1C=

1

2

AC•O1F=

1

2

AC•r1=3r1，S△BO1C=

1

2

BC•O1E=

1

2

BC•r1=4r1，S△AO1B=

1

2

AB•O1D=

1

2

AB•r1=5r1，S△ABC=

1

2

AC•BC=24．
又∵S△ABC=S△AO1C+S△BO1C+S△AO1B，
∴24=3r₁+4r₁+5r₁，
∴r₁=2．

（II）如图2，连接AO₁，BO₂，CO₁，CO₂，O₁O₂，则
S△AO1C=

1

2

AC•r2=3r2，S△BO2C=

1

2

BC•r2=4r2．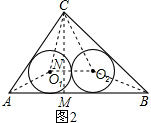
∵等圆⊙O₁，⊙O₂外切，
∴O₁O₂=2r₂，且O₁O₂∥AB．
过点C作CM⊥AB于点M，交O₁O₂于点N，则
CM=

AC•BC

AB

=

24

5

，CN=CM-r2=

24

5

-r2．
∴S△CO1O2=

1

2

O1O2•CN=(

24

5

-r2)r2，
∴S梯形AO1O2B=

1

2

(2r2+10)r2=(r2+5)r2．
∵S△ABC=S△AO1C+S△BO2C+S△CO1O2+S梯形AO1O2B，
∴3r₂+4r₂+（

24

5

-r₂）•r₂+（r₂+5）r₂=24，
解得r₂=

10

7

．

（III）如图3，连接AO₁，BO_n，CO₁，CO_n，O₁O_n，则
S△AO1C=

1

2

AC•rn=3rn，S△BOnC=

1

2

BC•rn=4rn．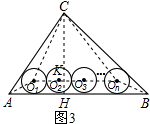
∵等圆⊙O₁，⊙O₂，…，⊙O_n依次外切，且均与AB边相切，
∴O₁，O₂，…，O_n均在直线O₁O_n上，且O₁O_n∥AB，
∴O₁O_n=（n-2）2r_n+2r_n=2（n-1）r_n．
过点C作CH⊥AB于点H，交O₁O_n于点K，
则CH=

24

5

，CK=

24

5

-rn．
S△CO1On=

1

2

O1On•CK=(n-1)(

24

5

-rn)rn，S梯形AO1OnB=

1

2

[2(n-1)rn+10]rn=[(n-1)rn+5]rn．
∵S△ABC=S△AO1C+S△BOnC+S△CO1On+S梯形AO1OnB，
∴24=3rn+4rn+(n-1)(

24

5

-rn)rn+[(n-1)rn+5]rn．
解得rn=

10

2n+3

．

点评：解决此题的方法是根据三角形的面积的不同计算方法进行计算．注意：直角三角形斜边上的高等于两条直角边的乘积除以斜边．