题目内容
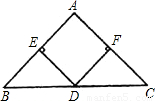
（2004•济南）如图，在△ABC中，AB=AC，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别为E、F．（1）求证：DE=DF；
（2）只添加一个条件，使四边形EDFA是正方形．请你至少写出两种不同的添加方法．（不另外添加辅助线，无需证明）
【答案】分析：（1）要证DE=DF，就要证△DEB≌△DFC，根据已知条件可达到目的；
（2）解决此题的关键是先假设四边形EDFA是正方形，根据其判定即可添加一个条件．
解答：（1）证明：∵DE⊥AB，DF⊥AC，
∴∠DEB=∠DFC=90°．
∵AB=AC，
∴∠B=∠C．
又∵DB=DC，△DEB≌△DFC（AAS），
∴DE=DF．
（2）解：添加∠A=90°．
∵四边形AFDE是矩形，
又∵DE=DF，
∴四边形EDFA是正方形．
（方法很多，如∠B=45°或BC=
AB或DE⊥DF或F为AC中点或DF∥AB等）
点评：此题考查了两个知识点：全等三角形的判定和正方形的判定．
（2）解决此题的关键是先假设四边形EDFA是正方形，根据其判定即可添加一个条件．
解答：（1）证明：∵DE⊥AB，DF⊥AC，
∴∠DEB=∠DFC=90°．
∵AB=AC，
∴∠B=∠C．
又∵DB=DC，△DEB≌△DFC（AAS），
∴DE=DF．
（2）解：添加∠A=90°．
∵四边形AFDE是矩形，
又∵DE=DF，
∴四边形EDFA是正方形．
（方法很多，如∠B=45°或BC=
AB或DE⊥DF或F为AC中点或DF∥AB等）点评：此题考查了两个知识点：全等三角形的判定和正方形的判定．
练习册系列答案
相关题目
