题目内容
如图，直角坐标系中，两条抛物线有相同的对称轴，下列关系式中不正确的是（ ）
A．h=m
B．n＞h
C．k＞n
D．h＞0，k＞0
【答案】分析：由抛物线的对称轴所在的位置判断出h，m、k、n的正负再根据实数比较大小的法则进行比较即可．
解答：解：①由函数y=
（x-h）2+k的图象可知，h＞0，k＞0，
由函数y=
（x-m）2+n的图象可知，m＞0，n＜0，
∵两抛物线有相同的对称轴，
∴h=m，故A正确；
②∵h＞0，n＜0，
∴h＞n，故B错误；
③∵k＞0，n＜0，
∴k＞n，故C正确；
④∵h＞0，k＞0，故D正确；
故选B．
点评：此题比较简单，考查的是抛物线的顶点式：y=a（x-
）2+
．
解答：解：①由函数y=
（x-h）2+k的图象可知，h＞0，k＞0，由函数y=
（x-m）2+n的图象可知，m＞0，n＜0，∵两抛物线有相同的对称轴，
∴h=m，故A正确；
②∵h＞0，n＜0，
∴h＞n，故B错误；
③∵k＞0，n＜0，
∴k＞n，故C正确；
④∵h＞0，k＞0，故D正确；
故选B．
点评：此题比较简单，考查的是抛物线的顶点式：y=a（x-
）2+． 
练习册系列答案
相关题目
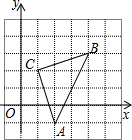如图，直角坐标系中，△ABC的顶点都在网格点上，其中，A点坐标为（2，-1），则△ABC的面积为
？若存在，请求出所有这样的点；若不存在，请说明理由．
在如图平面直角坐标系中，△ABC三个顶点A、B、C的坐标分别为A（2，-1），B（1，-3），C（4，-4），
如图，直角坐标系中，△ABC的顶点都在网格点上，C点坐标为（1，2），原来△ABC各个顶点纵坐标不变，横坐标都增加2，所得的三角形面积是
在如图的直角坐标系中，将△ABC平移后得到△A′B′C′，它们的个顶点坐标如表所示：