题目内容
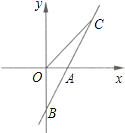
【题目】已知:如图,等腰△ABC中,AB=BC,AE⊥BC于点E,EF⊥AB于点F,若CE=1,![]() ,求EF的长.
,求EF的长.
【答案】![]()
【解析】
试题分析:Rt△ABE中,EF⊥AB,易得∠AEF=∠B,即cos∠B=![]() ,由此可求得BE、AB的比例关系,即BE、BC的比例关系,根据EC=BC﹣BE,即可求出BE、AE的长;然后根据∠AEF的余弦值,即可在Rt△AEF中,求出EF的长.
,由此可求得BE、AB的比例关系,即BE、BC的比例关系,根据EC=BC﹣BE,即可求出BE、AE的长;然后根据∠AEF的余弦值,即可在Rt△AEF中,求出EF的长.
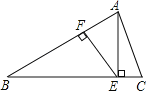
解:∵AE⊥BC,∴∠AEF+∠1=90°;
∵EF⊥AB,∴∠1+∠B=90°;
∴∠B=∠AEF;
∴![]()
∵在Rt△ABE中,∠AEB=90°
∴![]() ;
;
设BE=4k,AB=5k,∵BC=AB,∴EC=BC﹣BE=BA﹣BE=k;
∵EC=1,∴k=1;
∴BE=4,AB=5;
∴AE=3;(4分)
在Rt△AEF中,∠AFE=90°,
∵![]() ,
,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目