题目内容
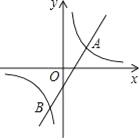
【题目】如图，反比例函数
（k≠0）图象经过点（1，2），并与直线y=2x+b交于点A（x1，y1），B（x2，y2），且满足（x1+x2）（1﹣x1x2）=3．
（1）求k的值；
（2）求b的值及点A，B的坐标．
【答案】（1）k=2；（2）b=﹣3，A（2，1），B（﹣
，﹣4）．
【解析】试题分析：（1）根据反比例函数性质，k为图象上点的坐标之积，易求k值．
（2）欲求b的值及点A，B的坐标，先求方程组
有两个不同解，根据一元二次方程根与系数关系即可求出．
试题解析：（1）∵反比例函数y=
（k≠0）图象经过点（1，2），
∴2=
k=2．
（2）由题意
2x2+bx﹣2=0①
△=b2+16＞0
， 
则由（x1+x2）（1﹣x1x2）=3
∴
∴b=﹣3．
∴①为2x2﹣3x﹣2=0
解得： 
， 
所以：y1=1，y2=﹣4．
即A（2，1），B（﹣
，﹣4）．
练习册系列答案
名校名卷单元同步训练测试题系列答案
相关题目
