题目内容
 如图,双曲线y=
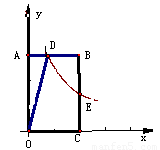
如图,双曲线y=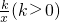 经过矩形OABC的边AB的中点D,交BC于点E.若四边形ODBE的面积为6.
经过矩形OABC的边AB的中点D,交BC于点E.若四边形ODBE的面积为6.
(1)试说明BE=CE;
(2)求k的值.
 解:(1)设点B的坐标为(a,b),
解:(1)设点B的坐标为(a,b),∵点D为AB的中点,
∴点D的坐标为(a,
 b),
b),∵点D在y=
 上,
上,∴
 b=
b= ,
,∴k=
 ab,
ab,设点E的坐标为(x,b)
∵E在双曲线y=
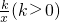 上,
上,∴b=
 ,
,∴x=
 a,
a,∴BE=CE;
(2)连接BO,由(1)可知D、E是AB、BC的中点,
S△OCE=S△OBE=S△OBD=S△DOA=
 S矩形OABC,
S矩形OABC,∵四边形ODBE的面积为6,
∴S矩形OCBA=12,
∴ab=12,
即k=
 ab=
ab= ×12=6.
×12=6.分析:(1)设点B的坐标为(a,b),再表示出点D的坐标,然后根据点D在y=
 上可得
上可得 b=
b= ,进而得到k=
,进而得到k= ab,设点E的坐标为(x,b)由E在双曲线y=
ab,设点E的坐标为(x,b)由E在双曲线y=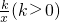 上,可得b=
上,可得b= ,进而得到x=
,进而得到x= a,进而得到BE=CE;
a,进而得到BE=CE;(2)根据题意可得S△OCE=S△OBE=S△OBD=S△DOA=
 S矩形OABC,由四边形ODBE的面积为6,可得矩形ABCO的面积为12,进而可以算出k的值.
S矩形OABC,由四边形ODBE的面积为6,可得矩形ABCO的面积为12,进而可以算出k的值.点评:此题主要考查了反比例函数图象上的点的坐标特征,关键是掌握图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
相关题目
 经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C,若点A的坐标为(-6,4),则△AOC的面积为
经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C,若点A的坐标为(-6,4),则△AOC的面积为
 经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与
经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与 轴正半轴的夹角,AB∥
轴正半轴的夹角,AB∥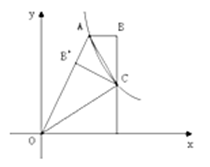
 经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为5,则k的值是 ▲ .
经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为5,则k的值是 ▲ .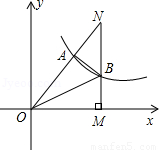
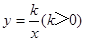 经过矩形QABC的边BC的中点E,交AB于点D。若梯形ODBC的面积为3,则双曲线的解析式为 ▲ .
经过矩形QABC的边BC的中点E,交AB于点D。若梯形ODBC的面积为3,则双曲线的解析式为 ▲ .