题目内容
 已知一次函数的图象经过A(-2,-3),B(1,3)两点.
已知一次函数的图象经过A(-2,-3),B(1,3)两点.
(1)求这个一次函数的解析式;
(2)试判断点P(-1,1)是否在这个一次函数的图象上;
(3)画出这个一次函数的图象;
(4)求此函数与x轴、y轴围成的三角形的面积.
解:(1)设函数的解析式是y=kx+b,
根据题意得: ,
,
解得: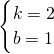 ,
,
则函数的解析式是:y=2x+1;
(2)当x=-1时,y=-1,故P(-1,1)不在函数的图象上;
(3)函数y=2x+1的图象如下:

(4)在y=2x+1中令x=0,解得:y=1,
令y=0,解得:x=- ,
,
故与y轴,x轴的交点分别是:(0,1)和(- ,0),
,0),
则三角形的面积是: ×1×
×1× =
= .
.
分析:(1)设函数的解析式是y=kx+b,把A(-2,-3),B(1,3)代入函数的解析式,然后解方程组即可求解;
(2)判断(-1,1)是否满足函数的解析式即可判断;
(3)作出过A、B的直线即可;
(4)求得函数与x轴、y轴的交点坐标,即求得三角形的两直角边长,利用三角形面积公式求解.
点评:本题考查了待定系数法求函数的解析式,以及函数的图象,函数的图象与解析式的关系,满足解析式的点一定在图象上,图象上的点的坐标一定满足函数解析式.
根据题意得:
 ,
,解得:
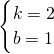 ,
,则函数的解析式是:y=2x+1;
(2)当x=-1时,y=-1,故P(-1,1)不在函数的图象上;
(3)函数y=2x+1的图象如下:

(4)在y=2x+1中令x=0,解得:y=1,
令y=0,解得:x=-
 ,
,故与y轴,x轴的交点分别是:(0,1)和(-
 ,0),
,0),则三角形的面积是:
 ×1×
×1× =
= .
.分析:(1)设函数的解析式是y=kx+b,把A(-2,-3),B(1,3)代入函数的解析式,然后解方程组即可求解;
(2)判断(-1,1)是否满足函数的解析式即可判断;
(3)作出过A、B的直线即可;
(4)求得函数与x轴、y轴的交点坐标,即求得三角形的两直角边长,利用三角形面积公式求解.
点评:本题考查了待定系数法求函数的解析式,以及函数的图象,函数的图象与解析式的关系,满足解析式的点一定在图象上,图象上的点的坐标一定满足函数解析式.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
 的图象与一次函数y=x+3的图象的交点坐标;
的图象与一次函数y=x+3的图象的交点坐标; 和反比例函数
和反比例函数 ,求这两个函数图象在同一坐标系内的交点坐标。
,求这两个函数图象在同一坐标系内的交点坐标。
 的图象与一次函数y=x+3的图象的交点坐标;
的图象与一次函数y=x+3的图象的交点坐标;