Question

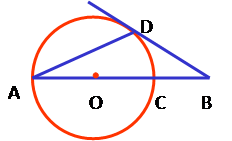
如图，线段AB经过圆心O，交⊙O于点A、C，∠B=30°，直线BD与⊙O切于点D，则∠ADB的度数是

120°

．

Answer 1

分析：连接OD，根据切线性质求出∠ODB，根据三角形内角和定理求出∠DOB，求出∠A，即可求出答案．

解答：解：
连接OD，
∵BD切⊙O于D，
∴∠ODB=90°，
∵∠B=30°，
∴∠DOB=60°，
∴∠A=

1

2

∠DOB=30°，
∴∠ADB=180°-∠B-∠A=180°-30°-30°=120°，
故答案为：120°．

点评：本题考查了切线的性质，三角形的内角和定理，圆周角定理的应用，主要考查学生的推理和计算能力，注意：圆的切线垂直于过切点的半径．