题目内容
（2013•石峰区模拟）如图所示，在半径为5的⊙O中，弦AB=6，点C是优弧 |
| AB |
| 3 |
| 5 |
| 3 |
| 5 |
分析：过B点作直径BD，连结AD，根据直径所对的圆周角为直角得到∠DAB=90°，再利用正弦的定义得到sin∠D=
=
，然后根据圆周角定理得到∠C=∠D，则sinC=
．
| AB |
| BD |
| 3 |
| 5 |
| 3 |
| 5 |
解答：解：过B点作直径BD，连结AD，如图，
∵BD为⊙O的直径，
∴∠DAB=90°，
在Rt△ABD中，AB=6，BD=10，
∴sin∠D=
=
=
，
∵∠C=∠D，
∴sinC=
．
故答案为
．
∵BD为⊙O的直径，
∴∠DAB=90°，
在Rt△ABD中，AB=6，BD=10，
∴sin∠D=
| AB |
| BD |
| 6 |
| 10 |
| 3 |
| 5 |
∵∠C=∠D，
∴sinC=
| 3 |
| 5 |
故答案为
| 3 |
| 5 |
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了圆周角定理的推论以及锐角三角函数的定义．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
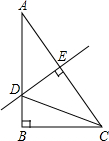（2013•石峰区模拟）如图．在Rt△ABC中，∠A=30°，DE垂直平分斜边AC，交AB于D，E为垂足，连接CD，若BD=1，则AC的长是
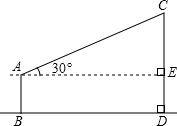（2013•石峰区模拟）如图所示，小明测量学校旗杆的高度，他在离电线杆CD距离为15米的地方放置一个高1.5米的测角仪（AB），此时，经A处测得旗杆上顶端C处的仰角为30°．请问：这样就能够测出旗杆CD的高度吗？如果能，CD的高是多少米？（结果精确到0.1）
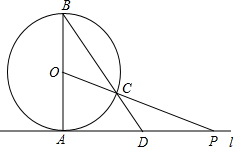（2013•石峰区模拟）如图，已知直线L与⊙O相切于点A，直径AB=6，点P在L上移动，连结OP交⊙O于点C，连结BC并延长BC交直线l于点D．