题目内容
 如图,某人沿着边长为40m的正方形,按A→B→C→D→A→…方向,甲从A以65米/分的速度,乙从B以72米/分的速度行走,当乙第一次追上甲时在正方形的
如图,某人沿着边长为40m的正方形,按A→B→C→D→A→…方向,甲从A以65米/分的速度,乙从B以72米/分的速度行走,当乙第一次追上甲时在正方形的
- A.AB边上
- B.DA边上
- C.BC边上
- D.CD边上
B
分析:路程问题中的同向同地同时出发,跑的快得要想和跑的慢的第一次相遇,需要多跑 圈.
圈.
解答:根据正方形的周长公式,正方形的周长是160米.根据甲、乙的速度知:乙每分钟比甲每分钟快7米.乙要想追上甲,需比甲多跑 圈,即120米.故需要
圈,即120米.故需要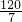 分钟.
分钟.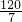 ×72÷160=7
×72÷160=7 .即当乙第一次追上甲时在正方形的DA边上.故选B.
.即当乙第一次追上甲时在正方形的DA边上.故选B.
点评:此题考查了平面图形,主要培养学生的观察能力.
分析:路程问题中的同向同地同时出发,跑的快得要想和跑的慢的第一次相遇,需要多跑
 圈.
圈.解答:根据正方形的周长公式,正方形的周长是160米.根据甲、乙的速度知:乙每分钟比甲每分钟快7米.乙要想追上甲,需比甲多跑
 圈,即120米.故需要
圈,即120米.故需要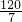 分钟.
分钟.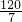 ×72÷160=7
×72÷160=7 .即当乙第一次追上甲时在正方形的DA边上.故选B.
.即当乙第一次追上甲时在正方形的DA边上.故选B.点评:此题考查了平面图形,主要培养学生的观察能力.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 如图,某人沿着边长为40m的正方形,按A→B→C→D→A→…方向,甲从A以65米/分的速度,乙从B以72米/分的速度行走,当乙第一次追上甲时在正方形的( )
如图,某人沿着边长为40m的正方形,按A→B→C→D→A→…方向,甲从A以65米/分的速度,乙从B以72米/分的速度行走,当乙第一次追上甲时在正方形的( )| A、AB边上 | B、DA边上 | C、BC边上 | D、CD边上 |

