题目内容
已知方程x2+(m+1)x-3=0和方程x2-4x-m=0有一个公共根,求这两个非公共根的和.
解:设方程x2+(m+1)x-3=0的两个根为α,β,则
α+β=-(m+1),αβ=-3,
∴α-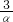 =-(m+1),
=-(m+1),
设方程x2-4x-m=0的根为α,γ,则α+γ=4,αγ=-m,
∴α(4-α)=-m,
∴α-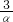 =α(4-α)-1,
=α(4-α)-1,
α2-3=α2(4-α)-α,
解得:α=3,
∴β=-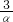 =-1,γ=4-α=4-3=1,
=-1,γ=4-α=4-3=1,
∴β+γ=0.
这两个非公共根的和是0.
分析:先设方程x2+(m+1)x-3=0的根为α,β,求出α+β=-(m+1),αβ=-3,得出α-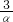 =-(m+1),再设方程x2-4x-m=0的根为α,γ,则α+γ=4,αγ=-m,根据题得出α-
=-(m+1),再设方程x2-4x-m=0的根为α,γ,则α+γ=4,αγ=-m,根据题得出α-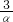 =α(4-α)-1,
=α(4-α)-1,
解出α的值,即可求出β和γ的值,从而得出两个非公共根的和.
点评:此题考查了一元二次方程的解,解题的关键是根据x1+x2=- ,x1x2=
,x1x2= 进行求解,难度适中.
进行求解,难度适中.
α+β=-(m+1),αβ=-3,
∴α-
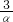 =-(m+1),
=-(m+1),设方程x2-4x-m=0的根为α,γ,则α+γ=4,αγ=-m,
∴α(4-α)=-m,
∴α-
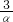 =α(4-α)-1,
=α(4-α)-1,α2-3=α2(4-α)-α,
解得:α=3,
∴β=-
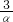 =-1,γ=4-α=4-3=1,
=-1,γ=4-α=4-3=1,∴β+γ=0.
这两个非公共根的和是0.
分析:先设方程x2+(m+1)x-3=0的根为α,β,求出α+β=-(m+1),αβ=-3,得出α-
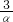 =-(m+1),再设方程x2-4x-m=0的根为α,γ,则α+γ=4,αγ=-m,根据题得出α-
=-(m+1),再设方程x2-4x-m=0的根为α,γ,则α+γ=4,αγ=-m,根据题得出α-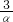 =α(4-α)-1,
=α(4-α)-1,解出α的值,即可求出β和γ的值,从而得出两个非公共根的和.
点评:此题考查了一元二次方程的解,解题的关键是根据x1+x2=-
 ,x1x2=
,x1x2= 进行求解,难度适中.
进行求解,难度适中. 
练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目