题目内容
如图,已知直线l1的解析式为y=3x+6,直线l1与x轴,y轴分别相交于A,B两点,直线l2经过B,C两点,点C的坐标为(8,0),又已知点P在x轴上从点A向点C移动,点Q在直线l2从点C 向点B移动.点P,Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t秒(1<t<10).
向点B移动.点P,Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t秒(1<t<10).(1)求直线l2的解析式;
(2)设△PCQ的面积为S,请求出S关于t的函数关系式;
(3)试探究:当t为何值时,△PCQ为等腰三角形?
分析:(1)因为l1过点B,所以代入直线l1的解析式求得点B的坐标,又因为直线l2经过B,C两点,所以将点B、C的坐标代入直线y=kx+b(k≠0),列方程组即可求得;
(2)过Q作QD⊥x轴于D,则△CQD∽△CBO,得出
=
,由题意,知OA=2,OB=6,OC=8,BC=
=10,得出
=
,故QD=
t,即可求得函数解析式;
(3)要想使△PCQ为等腰三角形,需满足CP=CQ,或QC=QP,或PC=PQ.
(2)过Q作QD⊥x轴于D,则△CQD∽△CBO,得出
| QD |
| BO |
| QC |
| BC |
| OB2+OC2 |
| QD |
| 6 |
| t |
| 10 |
| 3 |
| 5 |
(3)要想使△PCQ为等腰三角形,需满足CP=CQ,或QC=QP,或PC=PQ.
解答:解:(1)由题意,知B(0,6),C(8,0),
设直线l2的解析式为y=kx+b(k≠0),则
,
解得k=-
,b=6,
则l2的解析式为y=-
x+6;
 (2)解法一:如图,过P作PD⊥l2于D,
(2)解法一:如图,过P作PD⊥l2于D,
∵∠PDC=∠BOC=90°,∠DCP=∠OCB
∴△PDC∽△BOC
∴
=
由题意,知OA=2,OB=6,OC=8
∴BC=
=10,PD=10-t
∴
=
,
∴PD=
(10-t)
∴S△PCQ=
CQ•PD=
t•
(10-t)=-
t2+3t;
 解法二:如图,过Q作QD⊥x轴于D,
解法二:如图,过Q作QD⊥x轴于D,
∵∠QDC=∠BOC=90°,∠QCD=∠BCO
∴△CQD∽△CBO
∴
=
由题意,知OA=2,OB=6,OC=8
∴BC=
=10
∴
=
∴QD=
t
∴S△PCQ=
PC•QD=
(10-t)•
t=-
t2+3t;
(3)∵PC=10-t,CQ=t,
要想使△PCQ为等腰三角形,需满足CP=CQ,或QC=QP,或PC=PQ,
∴当CP=CQ时,由题10-t=t,得t=5(秒);
当QC=QP时,
=
,即
=
解得t=
(秒);
当PC=PQ时,
=
,即
=
,解得t=
(秒);
即t=5或
或
.
设直线l2的解析式为y=kx+b(k≠0),则
|
解得k=-
| 3 |
| 4 |
则l2的解析式为y=-
| 3 |
| 4 |
 (2)解法一:如图,过P作PD⊥l2于D,
(2)解法一:如图,过P作PD⊥l2于D,∵∠PDC=∠BOC=90°,∠DCP=∠OCB
∴△PDC∽△BOC
∴
| PD |
| BO |
| PC |
| BC |
由题意,知OA=2,OB=6,OC=8
∴BC=
| OB2+OC2 |
∴
| PD |
| 6 |
| 10-t |
| 10 |
∴PD=
| 3 |
| 5 |
∴S△PCQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 10 |
 解法二:如图,过Q作QD⊥x轴于D,
解法二:如图,过Q作QD⊥x轴于D,∵∠QDC=∠BOC=90°,∠QCD=∠BCO
∴△CQD∽△CBO
∴
| QD |
| BO |
| QC |
| BC |
由题意,知OA=2,OB=6,OC=8
∴BC=
| OB2+OC2 |
∴
| QD |
| 6 |
| t |
| 10 |
∴QD=
| 3 |
| 5 |
∴S△PCQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 10 |
(3)∵PC=10-t,CQ=t,
要想使△PCQ为等腰三角形,需满足CP=CQ,或QC=QP,或PC=PQ,
∴当CP=CQ时,由题10-t=t,得t=5(秒);
当QC=QP时,
| QC |
| BC |
| ||
| OC |
| t |
| 10 |
| ||
| 8 |
| 50 |
| 13 |
当PC=PQ时,
| ||
| OC |
| PC |
| BC |
| ||
| 8 |
| 10-t |
| 10 |
| 80 |
| 13 |
即t=5或
| 50 |
| 13 |
| 80 |
| 13 |
点评:此题考查了一次函数与三角形的综合知识,要注意待定系数法的应用,要注意数形结合思想的应用.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
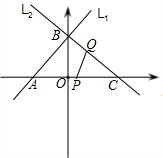 直线L2从点C向点B移动(一点到达终点,另一点即停止运动).点P、Q同时出发,移动的速度都为每秒1个单位长度,设移动时间为t秒.
直线L2从点C向点B移动(一点到达终点,另一点即停止运动).点P、Q同时出发,移动的速度都为每秒1个单位长度,设移动时间为t秒. 如图,已知直线l1的解析式为y=3x+6,直线l1,与x轴、y轴分别相交于A,B两点,直线l2经过B,C两点,点C的坐标为(8,0).又已知点P在x轴上从点A向点C移动,点Q在直线l2上从点C向点B移动,点P,Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t s(1<t<10).
如图,已知直线l1的解析式为y=3x+6,直线l1,与x轴、y轴分别相交于A,B两点,直线l2经过B,C两点,点C的坐标为(8,0).又已知点P在x轴上从点A向点C移动,点Q在直线l2上从点C向点B移动,点P,Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t s(1<t<10). B移动.点P、Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t秒(1<t<10).
B移动.点P、Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t秒(1<t<10).