��Ŀ����
����Ŀ���Ķ�������ϣ�
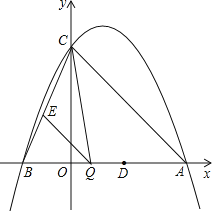
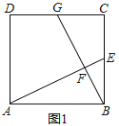
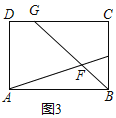
С����������һ�����⣺��ͼ1����������ABCD�У���E�DZ�BC���е㣬��F���߶�AE��һ�㣬BF���ӳ��߽�����CD�ڵ�G����AB=6��AF=4EF����CG��ֵ����AFB�Ķ�����
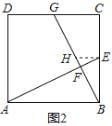
���������ǣ�����E��EH��AB��BG�ڵ�H���õ���BAF�ס�HEF����ͼ2����
��1��CG���ڶ��٣���AFB���ڶ��ٶȣ�
�ο�С��˼������ķ���������������⣻
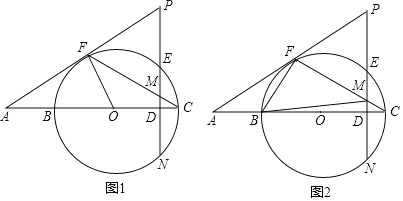
��2����ͼ3���ھ���ABCD�У���E�DZ�BC���е㣬��F���߶�AE��һ�㣬BF���ӳ��߽�����CD�ڵ�G����AF=3EF����![]() ��ֵ��
��ֵ��
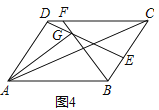
��3����ͼ4����ƽ���ı���ABCD�У�E��F�ֱ��DZ�BC��CD�ϵĵ㣬BF��DE�ཻ�ڵ�G����AB=kAD����DAG=��BAC�����![]() ��ֵ���ú�k��ʽ�ӱ�ʾ��
��ֵ���ú�k��ʽ�ӱ�ʾ��
���𰸡���1��CG=3����AFB=90������2��![]() ����3��
����3��![]() ��
��
��������
��1������E��EH��CD��BG�ڵ�H�����������ε����ʺ����������ε��ж������õ���EFH�ס�AFB���������������ε����ʵõ�CG=![]() AB=3��
AB=3��
��2�����գ�1���Ľ��˼·���㼴�ɣ�
��3���ӳ�AG��DC��M���ӳ�DE��AB���ӳ�����N���������������ε��ж����������ʶ������
��1������E��EH��CD��BG�ڵ�H��
���BEH�ס�BCG����![]() ��
��
�ߵ�E�DZ�BC���е㣬��BC=2BE����CG=2HE��
���ı���ABCD�������Σ���AB��CD��
��EH��AB�����EFH�ס�AFB��
��![]() ����AF=4EF����AB=4EH��
����AF=4EF����AB=4EH��
��CG=![]() AB=3����CD=6����CG=BE��
AB=3����CD=6����CG=BE��
����ABE����BCG��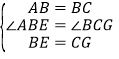 ��
��
���ABE�ա�BCG�����BAE=��CBG��
�ߡ�ABF+��CBG=90�������BAE+��ABF=90�������AFB=90����
��2����ͼ3��ͬ��1�������ó���CG=2HE��
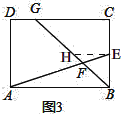
ͬ��1���ķ����ó���![]() ��
��
��AF=3EF����AB=3EH����EH=![]() AB��
AB��
��CG=2EH=![]() AB����
AB����![]() ��
��
��3���ӳ�AG��DC��M���ӳ�DE��AB���ӳ�����N��
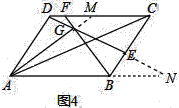
�ߡ�DAG=��BAC����ADM=��ABC��
���ADM�ס�ABC����![]() =k��
=k��
�ߵ�E�DZ�BC���е㣬��![]() ��
��
��DC��AB����E�DZ�BC���е㣬
��AB=DC=BN����DC��AB��
��![]() ��
��![]() ��
��
��![]() ����AB=
����AB=![]() AN��
AN��
��DF=![]() DM����
DM����![]() ��
��
��![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�