Question

如图，一艘轮船在海上以每小时36海里的速度向正西方向航行，上午8时，在B处测得小岛A在北偏东30°方向，之后轮船继续向正西方向航行，于上午9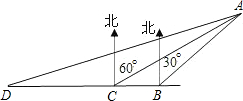时到达C处，这时测得小岛A在北偏东60°方向．如果轮船仍继续向正西方向航行，于上午11时到达D处，这时轮船与小岛A相距多远？

Answer 1

分析：作AE⊥BD于点E，根据条件可以得到∠ACB=∠CAB=30度，因而AB=BC=36海里，在直角△ADE中根据勾股定理就可以求解．

解答：解：作AE⊥BD于点E，
则∠ACB=90°-60°=30°，∠ABE=90°-30°=60°，
∵∠ABE=∠ACB+∠CAB
∴∠CAB=30°
∴∠ACB=∠CAB
∴AB=BC=36海里，
在直角△ABE中，∠ABE=60°，
∴AE=

3

2

AB=18

3

海里，BE=

1

2

AB=18海里，
在直角△ADE中，DE=126海里，
根据勾股定理得到AD=

1262+(18 3 )2

=

16848

=36

13

海里．

点评：本题主要考查了方向角含义，作出高线转化为直角三角形的问题是解题的关键．