题目内容
某服装店欲购甲、乙两种新款运动服,甲款每套进价350元,乙款每套进价200元,该店计划用不低于7600元且不高于8000元的资金订购30套甲、乙两款运动服.
(1)该店订购这两款运动服,共有哪几种方案?
(2)若该店以甲款每套450元,乙款每套320元的价格全部出售,哪种方案获利最大?
(1)该店订购这两款运动服,共有哪几种方案?
(2)若该店以甲款每套450元,乙款每套320元的价格全部出售,哪种方案获利最大?
考点:一次函数的应用,一元一次不等式组的应用
专题:
分析:(1)根据用不低于7600元且不高于8000元的资金订购30套甲、乙两款运动服,可得一元一次不等式组,解一元一次不等式组,可得答案;
(2)根据利润关系,可得一次函数,根据k的值,函数的性质,可得答案.
(2)根据利润关系,可得一次函数,根据k的值,函数的性质,可得答案.
解答:解:设该店订购甲款运动服x套,则订购乙款运动服(30-x)套,由题意,
(1)
解这个不等式组,得
≤x≤
.
∵x为整数,∴x取11,12,13.∴30-x取19,18,17.
答:该店订购这两款运动服,共有3种方案:①甲款11套,乙款19套;②甲款12套,乙款18套;③甲款13套,乙款17套;
(2)设该店全部出售甲、乙两款运动服后获利y元,则y=(450-350)x+(320-200)(30-x)=-20x+3600
∵k=-20<0,
∴y随x的增大而减小,
∴当x=11时,y最大,
答:方案一即甲款11套,乙款19套时,获利最大.
(1)
|
| 32 |
| 3 |
| 40 |
| 3 |
∵x为整数,∴x取11,12,13.∴30-x取19,18,17.
答:该店订购这两款运动服,共有3种方案:①甲款11套,乙款19套;②甲款12套,乙款18套;③甲款13套,乙款17套;
(2)设该店全部出售甲、乙两款运动服后获利y元,则y=(450-350)x+(320-200)(30-x)=-20x+3600
∵k=-20<0,
∴y随x的增大而减小,
∴当x=11时,y最大,
答:方案一即甲款11套,乙款19套时,获利最大.
点评:本题考查了一次函数的应用,(1)列不等式组是解题关键,(2)一次函数的性质是解题关键,注意x只能取11,12,13.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
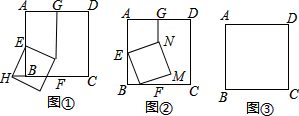
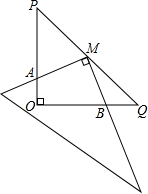 如图,在Rt△POQ中,OP=OQ,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.求证:MA=MB.
如图,在Rt△POQ中,OP=OQ,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.求证:MA=MB. 实践操作:如图,△ABC是直角三角形,∠ABC=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
实践操作:如图,△ABC是直角三角形,∠ABC=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).