题目内容
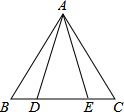 如图,△ABD≌△ACE,∠B=50°,∠AEC=110°,则∠DAE=
如图,△ABD≌△ACE,∠B=50°,∠AEC=110°,则∠DAE=
- A.30°
- B.40°
- C.50°
- D.60°
B
分析:根据全等三角形的对应角相等,三角形内角和定理来求∠DAE的度数.
解答:∵如图,△ABD≌△ACE,∠B=50°,
∴∠C=∠B=50°,∠BAD=∠CAE.
又∵∠C+∠AEC+∠CAE=180°,∠AEC=110°,
∴∠BAD=∠CAE=20°,
∴∠BAD+∠CAE+∠DAE+∠B+∠C=180°,即20°+20°+∠DAE+50°+50°=180°,
∴∠DAE=40°.
故选B.
点评:本题考查了全等三角形的性质;解答时,除必备的知识外,还应将条件和所求联系起来,即将所求的角与已知角通过全等及三角形内角之间的关系联系起来.
分析:根据全等三角形的对应角相等,三角形内角和定理来求∠DAE的度数.
解答:∵如图,△ABD≌△ACE,∠B=50°,
∴∠C=∠B=50°,∠BAD=∠CAE.
又∵∠C+∠AEC+∠CAE=180°,∠AEC=110°,
∴∠BAD=∠CAE=20°,
∴∠BAD+∠CAE+∠DAE+∠B+∠C=180°,即20°+20°+∠DAE+50°+50°=180°,
∴∠DAE=40°.
故选B.
点评:本题考查了全等三角形的性质;解答时,除必备的知识外,还应将条件和所求联系起来,即将所求的角与已知角通过全等及三角形内角之间的关系联系起来.

练习册系列答案
相关题目
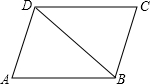 如图,△ABD≌△CDB,下面结论中不正确的是( )
如图,△ABD≌△CDB,下面结论中不正确的是( )| A、△ABD和△CDB的面积相等 | B、∠A+∠ABD=∠C+∠CBD | C、△ABD和△CDB的周长相等 | D、AD∥BC,且AD=BC |
 4、如图,∠ABD=90°,直线
4、如图,∠ABD=90°,直线 15、如图,∠ABD=∠CBD,DF∥AB,DE∥BC,则∠1与∠2的大小关系是
15、如图,∠ABD=∠CBD,DF∥AB,DE∥BC,则∠1与∠2的大小关系是 如图,△ABD中,点C、F分别为BD、AB上一点,AC、DF交于E,且CD=2BC,AE=2CE.求
如图,△ABD中,点C、F分别为BD、AB上一点,AC、DF交于E,且CD=2BC,AE=2CE.求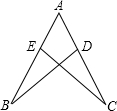 如图,△ABD≌△ACE,那么点B与点
如图,△ABD≌△ACE,那么点B与点