题目内容
【题目】已知在平面直角坐标系中点A(a,b),点B(a,0)的坐标满足|![]() a-b|+(a-4)2=0
a-b|+(a-4)2=0
(1)求点A、点B的坐标;
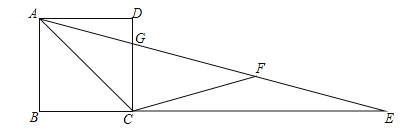
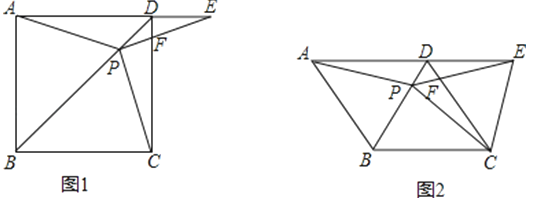
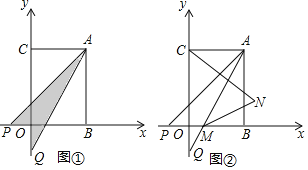
(2)已知点C(0,b),点P从B点出发沿x轴负方向以1个单位每秒的速度移动,同时,点Q从C点出发,沿y轴负方向以1.5个单位每秒的速度移动.某一时刻,如图①所示,且S阴=![]() S四边形OCAB,求点P移动的时间;
S四边形OCAB,求点P移动的时间;
(3)在(2)的条件和结论下,如图②所示,设AQ交轴于点M,作∠ACO、∠AMB的角平分线交于点N,求此时![]() 的值.
的值.
【答案】(1)A(4,6),B(4,0);(2)6;(3)![]() .
.
【解析】
(1)根据非负数的性质,根据方程组即可解决问题;
(2)设点P的运动时间为t秒.则BP=t,CQ=1.5t,QH=AC=4,AH=CQ=1.5t,根据S阴=S△APB+S矩形OBHQ-S△AQH,构建方程即可解决问题;
(3)由(2)可知,BP=t=6=AB,推出△ABP为等腰直角三角形,推出∠APB=45°,由CN平分∠ACQ,MN平分∠AMB,推出∠ACN=![]() ×90°=45°,∠BMN=
×90°=45°,∠BMN=![]() ∠AMB,推出∠APB=∠ACN=45°,过点N作NG∥AC,则∠CNG=∠ACN=45°=∠APB,可得∠GNM=∠NMB=
∠AMB,推出∠APB=∠ACN=45°,过点N作NG∥AC,则∠CNG=∠ACN=45°=∠APB,可得∠GNM=∠NMB=![]() ∠AMB,推出∠CNM-∠APB=∠CNM-45°=∠CNM-∠CNG=∠GNM=∠NMB=
∠AMB,推出∠CNM-∠APB=∠CNM-45°=∠CNM-∠CNG=∠GNM=∠NMB=![]() ∠AMB,即可得出结论.
∠AMB,即可得出结论.
(1)∵|![]() a-b|+(a-4)2=0
a-b|+(a-4)2=0
∴|![]() a-b|≥0,(a-4)2≥0,
a-b|≥0,(a-4)2≥0,
∴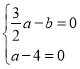 ,
,
解得![]() ,
,
∴A(4,6),B(4,0).
(2)由(1)可知,C(0,6),四边形OCAB是矩形,AC=4,AB=6,
过点Q作QH⊥AB于H.

设点P的运动时间为t秒.则BP=t,CQ=1.5t,QH=AC=4,AH=CQ=1.5t,
S阴=S△APB+S矩形OBHQ-S△AQH
=![]() ×6t+4(1.5t-6)-
×6t+4(1.5t-6)-![]() ×4×1.5t
×4×1.5t
=6t-24,
∵S阴=![]() S四边形OCAB,
S四边形OCAB,
∴6t-24=![]() ×4×6,
×4×6,
∴t=6.
(3)由(2)可知,BP=t=6=AB,
∴△ABP为等腰直角三角形,
∴∠APB=45°,
∵CN平分∠ACQ,MN平分∠AMB,
∴∠CN=![]() ×90°=45°,∠BMN=
×90°=45°,∠BMN=![]() ∠AMB,
∠AMB,
∴∠APB=∠ACN=45°,
过点N作NG∥AC,则∠CNG=∠ACN=45°=∠APB
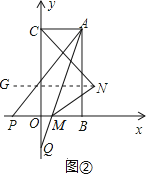
∵AC∥x轴,NG∥x轴,
∴∠GNM=∠NMB=![]() ∠AMB,
∠AMB,
∴∠CNM-∠APB=∠CNM-45°=∠CNM-∠CNG=∠GNM=∠NMB=![]() ∠AMB,
∠AMB,
∴![]() =
=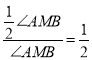 .
.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案【题目】李红在学校的研究性学习小组中负责了解初一年级200名女生掷实心球的测试成绩.她从中随机调查了若干名女生的测试成绩(单位:米),并将统计结果绘制成了如下的统计图表(内容不完整).
测试成绩 |
|
|
|
|
| 合计 |
频数 | 3 | 27 | 9 | m | 1 | n |

请你结合图表中所提供的信息,回答下列问题:
(1)表中m= ,n= ;
(2)请补全频数分布直方图;
(3)在扇形统计图中,![]() 这一组所占圆心角的度数为 度;
这一组所占圆心角的度数为 度;
(4)如果掷实心球的成绩达到6米或6米以上为优秀,请你估计该校初一年级女生掷实心球的成绩达到优秀的总人数.
【题目】2015年3月30日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
频率分布表
分数段 | 频数 | 频率 |
50.5~60.5 | 16 | 0.08 |
60.5~70.5 | 40 | 0.2 |
70.5~80.5 | 50 | 0.25 |
80.5~90.5 | m | 0.35 |
90.5~100.5 | 24 | n |
(1)这次抽取了 名学生的竞赛成绩进行统计,其中:m= ,n= ;
(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?