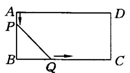
题目内容
如图26-3-14所示,在矩形ABCD中,AB=6cm,BC=12cm,点P从A点出发,沿AB边向点B以1cm/s的速度移动,同时,Q点从B点出发,沿BC边向点C以2cm/s的速度移动.如果P、Q两点分别到达B、C两点后就停止移动,解答下列问题:
(1)运动开始后第几秒时,△PBQ的面积等于8cm2?
(2)设运动开始后第t秒时,五边形APQCD的面积为Scm2,写出S与t的函数关系式,并指出自变量的取值范围.

(1)设运动开始后第xs时,△PBQ的面积等于8cm2,
根据题意,得![]() ·(6-x)·2x=8,
·(6-x)·2x=8,
∴x2-6x+8=0,
∴x1=4,x2=2.
答:运动开始后第2s或第4s时,△PBQ的面积等于8cm2.
(2)由题意得S=6×12-![]() (6-t)·2t,∴S=t2-6t+72(0<t<6).
(6-t)·2t,∴S=t2-6t+72(0<t<6).
点拨:在实际应用中,应注意自变量取值范围不再是全体实数这一根据所在.

练习册系列答案
相关题目
 已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克.
已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克.