题目内容
 如图⊙A的圆心在⊙O上,且与⊙O的内接△ABC的边切于点D,⊙A的半径为r,⊙O的半径为R,则此时AB、AC与R、r满足的关系式为:________.
如图⊙A的圆心在⊙O上,且与⊙O的内接△ABC的边切于点D,⊙A的半径为r,⊙O的半径为R,则此时AB、AC与R、r满足的关系式为:________.
AB•AC=2Rr
分析:连接AD、OA、OB,过点O作OE⊥AB,根据圆周角定理,∠AOB=2∠C,由等腰三角形的性质得∠AOE= ∠AOB,可证出△AOE∽△ACD,则
∠AOB,可证出△AOE∽△ACD,则 =
= ,从而得出AB、AC与R、r的关系.
,从而得出AB、AC与R、r的关系.
解答: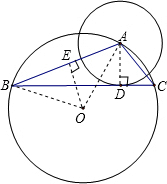 解:如图,
解:如图,
连接AD、OA、OB,过点O作OE⊥AB,
∴∠AEO=90°
∵BC是⊙A的切线,∴∠ADC=90°,
∵OA=OB,∴∠AOE=∠BOE,AE=BE
∵∠AOB=2∠C,
∴∠AOE=∠C,
∴△AOE∽△ACD,∴ =
= ,
,
∵⊙A的半径为r,⊙O的半径为R,
∴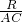 =
=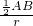 ,
,
∴AB•AC=2Rr.
故答案为AB•AC=2Rr.
点评:本题考查了切线的性质、圆周角定理和相似三角形的判定和性质,是基础知识要熟练掌握.
分析:连接AD、OA、OB,过点O作OE⊥AB,根据圆周角定理,∠AOB=2∠C,由等腰三角形的性质得∠AOE=
 ∠AOB,可证出△AOE∽△ACD,则
∠AOB,可证出△AOE∽△ACD,则 =
= ,从而得出AB、AC与R、r的关系.
,从而得出AB、AC与R、r的关系.解答:
 解:如图,
解:如图,连接AD、OA、OB,过点O作OE⊥AB,
∴∠AEO=90°
∵BC是⊙A的切线,∴∠ADC=90°,
∵OA=OB,∴∠AOE=∠BOE,AE=BE
∵∠AOB=2∠C,
∴∠AOE=∠C,
∴△AOE∽△ACD,∴
 =
= ,
,∵⊙A的半径为r,⊙O的半径为R,
∴
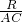 =
=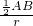 ,
,∴AB•AC=2Rr.
故答案为AB•AC=2Rr.
点评:本题考查了切线的性质、圆周角定理和相似三角形的判定和性质,是基础知识要熟练掌握.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 (2012•黄埔区一模)如图⊙P的圆心P在⊙O上,⊙O的弦AB所在的直线与⊙P切于C,若⊙P的半径为r,⊙O的半径为R.⊙O和⊙P的面积比为9:4,且PA=10,PB=4.8,DE=5,C、P、D三点共线.
(2012•黄埔区一模)如图⊙P的圆心P在⊙O上,⊙O的弦AB所在的直线与⊙P切于C,若⊙P的半径为r,⊙O的半径为R.⊙O和⊙P的面积比为9:4,且PA=10,PB=4.8,DE=5,C、P、D三点共线.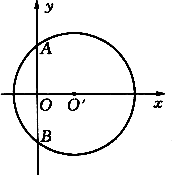

 ;
;
 ;
;