题目内容
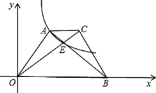
【题目】如图直线![]() 对应的函数表达式为
对应的函数表达式为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .直线
.直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,且经过点
,且经过点![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() .
.
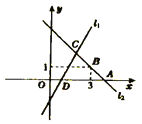
(1)求点![]() ,点
,点![]() 的坐标;
的坐标;
(2)求直线![]() 对应的函数表达式;
对应的函数表达式;
(3)求![]() 的面积;
的面积;
(4)利用函数图象写出关于![]() ,
,![]() 的二元一次方程组
的二元一次方程组![]() 的解.
的解.
【答案】(1)点D的坐标为(1,0),点C的坐标为(2,2);(2)![]() ;(3)3;(4)
;(3)3;(4)![]()
【解析】
(1)将y=0代入直线![]() 对应的函数表达式中即可求出点D的坐标,将点
对应的函数表达式中即可求出点D的坐标,将点![]() 代入直线
代入直线![]() 对应的函数表达式中即可求出点C的坐标;
对应的函数表达式中即可求出点C的坐标;
(2)根据图象可知点B的坐标,然后将点B和点C的坐标代入![]() 中,即可求出直线
中,即可求出直线![]() 对应的函数表达式;
对应的函数表达式;
(3)过点C作CE⊥x轴,先求出点A的坐标,然后根据三角形的面积公式求面积即可;
(4)根据二元一次方程组的解和两个一次函数交点坐标关系即可得出结论.
解:(1)将y=0代入![]() 中,解得x=1
中,解得x=1
∴点D的坐标为(1,0)
将点![]() 代入
代入![]() 中,得
中,得
![]()
解得:![]()
∴点C的坐标为(2,2);
(2)由图象可知:点B的坐标为(3,1)
将点B和点C的坐标代入![]() 中,得
中,得
![]()
解得:![]()
∴直线![]() 对应的函数表达式为
对应的函数表达式为![]() ;
;
(3)过点C作CE⊥x轴于E,

将y=0代入![]() 中,解得x=4
中,解得x=4
∴点A的坐标为(4,0)
∵点D(1,0),点C(2,2)
∴AD=4-1=3,CE=2
∴S△ADC=![]() ;
;
(4)∵直线![]() ,
,![]() 交于点
交于点![]()
∴关于![]() ,
,![]() 的二元一次方程组
的二元一次方程组![]() 的解为
的解为![]() .
.

练习册系列答案
相关题目