题目内容
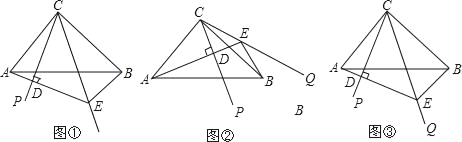
【题目】如图,一张矩形纸片![]() .点
.点![]() 在这张矩形纸片的边
在这张矩形纸片的边![]() 上,将纸片折叠,使
上,将纸片折叠,使![]() 落在射线
落在射线![]() 上,折痕为
上,折痕为![]() ,点
,点![]() 分别落在点
分别落在点![]() 处,
处,
(1)若![]() ,则
,则![]() 的度数为 °;
的度数为 °;
(2)若![]() ,求
,求![]() 的长.
的长.

【答案】(1)![]() ;(2)3
;(2)3
【解析】
(1)根据折叠可得∠BFG=∠GFB′,再根据矩形的性质可得∠DFC=40°,从而∠BFG=70°即可得到结论;
(2) 首先求出GD=9-![]() =
=![]() ,由矩形的性质得出AD∥BC,BC=AD=9,由平行线的性质得出∠DGF=∠BFG,由翻折不变性可知,∠BFG=∠DFG,证出∠DFG=∠DGF,由等腰三角形的判定定理证出DF=DG=
,由矩形的性质得出AD∥BC,BC=AD=9,由平行线的性质得出∠DGF=∠BFG,由翻折不变性可知,∠BFG=∠DFG,证出∠DFG=∠DGF,由等腰三角形的判定定理证出DF=DG=![]() ,再由勾股定理求出CF,可得BF,再利用翻折不变性,可知FB′=FB,由此即可解决问题.
,再由勾股定理求出CF,可得BF,再利用翻折不变性,可知FB′=FB,由此即可解决问题.
(1)根据折叠可得∠BFG=∠GFB′,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DGF=∠BFG,∠ADF=∠DFC,
∵![]()
∴∠DFC=40°
∴∠BFD=140°
∴∠BFG=70°
∴∠DGF=70°;
(2)∵AG=![]() ,AD=9,
,AD=9,
∴GD=9-![]() =
=![]() ,
,
∵四边形ABCD是矩形,
∴AD∥BC,BC=AD=9,
∴∠DGF=∠BFG,
由翻折不变性可知,∠BFG=∠DFG,
∴∠DFG=∠DGF,
∴DF=DG=![]() ,
,
∵CD=AB=4,∠C=90°,
∴在Rt△CDF中,由勾股定理得: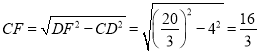 ,
,
∴BF=BC-CF=9-![]() ,
,
由翻折不变性可知,FB=FB′=![]() ,
,
∴B′D=DF-FB′=![]() -
-![]() =3.
=3.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目