题目内容
已知x1x2是方程x2-mx-1=0的两个根,且x1<x2,若x2≥2,
(1)求m的取值范围;
(2)若 +
+ =2,求m的值.
=2,求m的值.
解:(1)∵x1x2是方程x2-mx-1=0的两个根,且x1<x2,x2≥2,
∴当x=2时原方程的值小于等于0,即22-2m-1=0,解得m≥ ;
;
(2)∵x1x2是方程x2-mx-1=0的两个根,
∴x1+x2=m①,x1•x2=-1②,
∵原式=若 +
+ =
=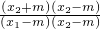 +
+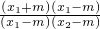 =2,即
=2,即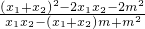 =2,
=2,
把①②代入得,2-m2=2,
解得m=±2,
∵m≥ ,
,
∴m=2.
分析:(1)先根据方程有两个实数根且x1<x2,x2≥2可知当x=2时原方程的值小于等于0,把x=2代入原方程即可求出m的取值范围;
(2)先用m表示出x1+x2与x1•x2的表达式,再把原分式方程通分,把x1+x2与x1•x2的值代入即可得出关于m的方程,求出m的值即可.
点评:本题考查的是根与系数的关系及解分式方程,解答(2)时要注意m的取值范围,这是此题的易错点.
∴当x=2时原方程的值小于等于0,即22-2m-1=0,解得m≥
 ;
;(2)∵x1x2是方程x2-mx-1=0的两个根,
∴x1+x2=m①,x1•x2=-1②,
∵原式=若
 +
+ =
=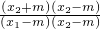 +
+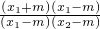 =2,即
=2,即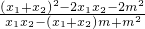 =2,
=2,把①②代入得,2-m2=2,
解得m=±2,
∵m≥
 ,
,∴m=2.
分析:(1)先根据方程有两个实数根且x1<x2,x2≥2可知当x=2时原方程的值小于等于0,把x=2代入原方程即可求出m的取值范围;
(2)先用m表示出x1+x2与x1•x2的表达式,再把原分式方程通分,把x1+x2与x1•x2的值代入即可得出关于m的方程,求出m的值即可.
点评:本题考查的是根与系数的关系及解分式方程,解答(2)时要注意m的取值范围,这是此题的易错点.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
填表解题:
| 方程 | 两根x1,x2 | x1+x2= | x1x2= |
| x2+2x+1=0 | |||
| x2-3x-4=0 | |||
| x2+4x-7=0 |
利用你的猜想解下列问题:
(1)若x1,x2是方程x2-2x-3=0的两根求,x12+x22和(x1+2)(x2+2)的值.
(2)已知2+
 是方程x2-4x+c=0的一个根,求方程的另一个根及c的值.
是方程x2-4x+c=0的一个根,求方程的另一个根及c的值.
填表解题:
上表你能猜想若x1,x2是方程ax2+bx+c=0(a不等0)的两根则x1+x2=______,x1x2=______
利用你的猜想解下列问题:
(1)若x1,x2是方程x2-2x-3=0的两根求,x12+x22和(x1+2)(x2+2)的值.
(2)已知2+ 是方程x2-4x+c=0的一个根,求方程的另一个根及c的值.
是方程x2-4x+c=0的一个根,求方程的另一个根及c的值.
| 方程 | 两根x1,x2 | x1+x2= | x1x2= |
| x2+2x+1=0 | |||
| x2-3x-4=0 | |||
| x2+4x-7=0 |
利用你的猜想解下列问题:
(1)若x1,x2是方程x2-2x-3=0的两根求,x12+x22和(x1+2)(x2+2)的值.
(2)已知2+
 是方程x2-4x+c=0的一个根,求方程的另一个根及c的值.
是方程x2-4x+c=0的一个根,求方程的另一个根及c的值. =4.
=4.