题目内容
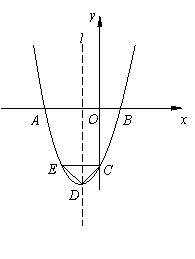
 如图,已知:抛物线与坐标轴相交于点A、B、C,顶点D的坐标为D(-1,4),又知C(-4,0)
如图,已知:抛物线与坐标轴相交于点A、B、C,顶点D的坐标为D(-1,4),又知C(-4,0)(1)求此抛物线的解析式.
(2)设直线BD与y轴相交于点E,求线段AE的长.
(3)设P(t,0)是线段CB上的一个动点,用S表示四边形CPED的面积.试求S关于t的函数关系式,写出自变量t的取值范围.
分析:(1)利用顶点式将顶点D的坐标为D(-1,4),代入解析式进而得出a的值即可;
(2)在y=-
(x+1)2+4中令x=0得:y=
,再求出直线BD的解析式求出线段AE的长即可;
(3)首先得出S△PBE=
BP×OE=
(2-t)×
=
-
t,又S△BCD=
×6×4=12,即可得出四边形CPED的面积S.
(2)在y=-
| 4 |
| 9 |
| 32 |
| 9 |
(3)首先得出S△PBE=
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 1 |
| 2 |
解答:解:(1)∵顶点D的坐标为D(-1,4),
∴设抛物线的解析式为y=a(x+1)2+4又知抛物线过C(-4,0),
∴0=a(-4+1)2+4,
∴解得:a=-
,
∴此抛物线的解析式为y=-
(x+1)2+4.
(2)在y=-
(x+1)2+4中令x=0得:y=
,
∴A(0,
),∴OA=
,
当0=-
(x+1)2+4,
解得:x1=-4,x2=2,
可求得B(2,0)设直线BD的解析式为y=kx+b,
得
,
解得
,
故直线BD的解析式为:y=-
x+
,
∵当x=0,y=
,
∴E(0,
),
∴线段AE的长=
-
=
.
(3)如图,
∵P(t,0)是线段CB上的一个动点,
∴BP=2-t
∴S△PBE=
BP×OE=
(2-t)×
=
-
t,
又S△BCD=
×6×4=12,
∴四边形CPED的面积S=
+
t(-4<t<2).
∴设抛物线的解析式为y=a(x+1)2+4又知抛物线过C(-4,0),
∴0=a(-4+1)2+4,
∴解得:a=-
| 4 |
| 9 |
∴此抛物线的解析式为y=-
| 4 |
| 9 |
(2)在y=-
| 4 |
| 9 |
| 32 |
| 9 |
∴A(0,
| 32 |
| 9 |
| 32 |
| 9 |
当0=-
| 4 |
| 9 |
解得:x1=-4,x2=2,
可求得B(2,0)设直线BD的解析式为y=kx+b,
得
|
解得
|
故直线BD的解析式为:y=-
| 4 |
| 3 |
| 8 |
| 3 |

∵当x=0,y=
| 8 |
| 3 |
∴E(0,
| 8 |
| 3 |
∴线段AE的长=
| 32 |
| 9 |
| 8 |
| 3 |
| 8 |
| 9 |
(3)如图,
∵P(t,0)是线段CB上的一个动点,
∴BP=2-t
∴S△PBE=
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
又S△BCD=
| 1 |
| 2 |
∴四边形CPED的面积S=
| 28 |
| 3 |
| 4 |
| 3 |
点评:此题主要考查了二次函数的综合应用以及待定系数法求一次函数解析式等知识,根据直线BD的解析式是解题关键.

练习册系列答案
相关题目
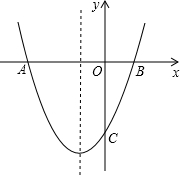 (2011•利川市一模)如图,已知:抛物线y=ax2+bx-4(a≠0)与x轴交于A、B两点,与y轴交于点C,A、B两点的坐标分别为A(-6,0)、B(2,0).
(2011•利川市一模)如图,已知:抛物线y=ax2+bx-4(a≠0)与x轴交于A、B两点,与y轴交于点C,A、B两点的坐标分别为A(-6,0)、B(2,0).