题目内容
如图,已知⊙P圆心P在直线y=2x-1的图象上运动.(1)若⊙P的半径为2,当⊙P与x轴相切时,求P点的坐标;
(2)若⊙P的半径为2,当⊙P与y轴相切时,求P点的坐标;
(3)若⊙P与x轴和y轴都相切时,⊙P的半径是多少?

【答案】分析:(1)当⊙P与x轴相切时,则P点到x轴的距离等于半径2.因为P在直线上,所以P点纵坐标是2或-2,再求横坐标即可;
(2)同理可求当⊙P与y轴相切时,P点的坐标;
(3)若⊙P与x轴和y轴都相切时,P到两坐标轴的距离相等,即横坐标和纵坐标相等.求出P点坐标,便知半径.
解答:解:(1)当⊙P与x轴相切时,P点的纵坐标为2或-2.
∴2=2x-1,
或-2=2x-1;
∴ .
.
∴P点的坐标为 或
或 .
.
(2)当⊙P与y轴相切时,P点的横坐标2或-2.
∴y=2×2-1=3,或y=2×(-2)-1=-5.
∴P点的坐标为(2,3)或(-2,-5).
(3)⊙P与x轴和y轴都相切时,横坐标与纵坐标绝对值相等
即x=y,或y=-x
∴x=2x-1,即x=1,y=1;或-x=2x-1,即x= ,y=-
,y=- ;
;
∴P点的坐标为(1,1)或( ,-
,- ),即⊙P的半径是1或
),即⊙P的半径是1或 .
.
点评:此题重点考查了直线与圆相切时的性质.直线与圆相切,则圆心到直线的距离等于圆的半径.
(2)同理可求当⊙P与y轴相切时,P点的坐标;
(3)若⊙P与x轴和y轴都相切时,P到两坐标轴的距离相等,即横坐标和纵坐标相等.求出P点坐标,便知半径.
解答:解:(1)当⊙P与x轴相切时,P点的纵坐标为2或-2.
∴2=2x-1,
或-2=2x-1;
∴
 .
.∴P点的坐标为
 或
或 .
.(2)当⊙P与y轴相切时,P点的横坐标2或-2.
∴y=2×2-1=3,或y=2×(-2)-1=-5.
∴P点的坐标为(2,3)或(-2,-5).
(3)⊙P与x轴和y轴都相切时,横坐标与纵坐标绝对值相等
即x=y,或y=-x
∴x=2x-1,即x=1,y=1;或-x=2x-1,即x=
 ,y=-
,y=- ;
;∴P点的坐标为(1,1)或(
 ,-
,- ),即⊙P的半径是1或
),即⊙P的半径是1或 .
.点评:此题重点考查了直线与圆相切时的性质.直线与圆相切,则圆心到直线的距离等于圆的半径.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
如图,已知圆心为A,B,C的三个圆彼此相切,且均与直线l相切.若⊙A,⊙B,⊙C的半径分别为a,b,c(0<c<a<b),则a,b,c一定满足的关系式为( )
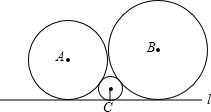

| A、2b=a+c | ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
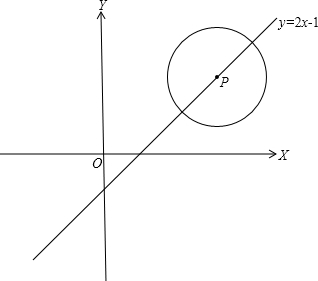 如图,已知⊙P圆心P在直线y=2x-1的图象上运动.
如图,已知⊙P圆心P在直线y=2x-1的图象上运动. 如图,已知圆心A(0,3),⊙A与x轴相切,⊙B的圆心在x轴的正半轴上,且⊙B与⊙A外切于点P,两圆的公切线MP交y轴于点M,交x轴于点N.
如图,已知圆心A(0,3),⊙A与x轴相切,⊙B的圆心在x轴的正半轴上,且⊙B与⊙A外切于点P,两圆的公切线MP交y轴于点M,交x轴于点N. (2013•太仓市二模)如图,已知圆心为C(0,1)的圆与y轴交于A,B两点,与x轴交于D,E两点,且DE=4
(2013•太仓市二模)如图,已知圆心为C(0,1)的圆与y轴交于A,B两点,与x轴交于D,E两点,且DE=4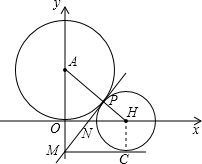 ⊙A外切于点P,两圆的公切线MP交y轴于点M,交x轴于点N.
⊙A外切于点P,两圆的公切线MP交y轴于点M,交x轴于点N. ,求直线MP的解析式及经过M、N、B三点的抛物线的解析式.
,求直线MP的解析式及经过M、N、B三点的抛物线的解析式.