题目内容
如图,直线y=﹣2x+4与坐标轴分别交于C、B两点,过点C作CD⊥x轴,点P是x轴下方直线CD上的一点,且△OCP与△OBC相似,求过点P的双曲线解析式.
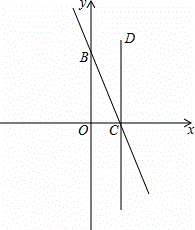
解:∵直线y=﹣2x+4与坐标轴分别交于C、B两点,
∴令y=0,可得﹣2x+4=0,解得x=2,即C(2,0),OC=2,
令x=0,可得y=4,即B(0,4),OB=4,
①如图1,当∠OBC=∠COP时,△OCP与△OBC相似,
∴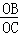 =
=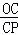 ,即
,即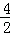 =
= ,解得CP=2,
,解得CP=2,
∴P(2,﹣1),
设过点P的双曲线解析式y=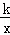 ,把P点代入得﹣1=
,把P点代入得﹣1=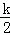 ,解得k=﹣2,
,解得k=﹣2,
∴过点P的双曲线解析式y= ,
,
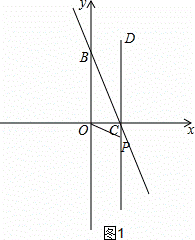
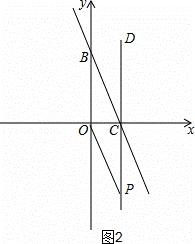
②如图2,当∠OBC=∠CPO时,△OCP与△OBC相似,
在△OCP和△COB中,
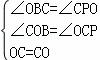
∴△OCP≌△COB(AAS)
∴CP=BO=4,
∴P(2,﹣4)
设过点P的双曲线解析式y=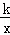 ,把P点代入得﹣4=
,把P点代入得﹣4=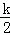 ,解得k=﹣8,
,解得k=﹣8,
∴过点P的双曲线解析式y=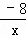 ,
,

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,在△ABC中,点D是边AB上一点,点E是边AC上一点,且DE∥BC,∠B=40°,∠AED=60°,则∠A的度数是( )
,在△ABC中,点D是边AB上一点,点E是边AC上一点,且DE∥BC,∠B=40°,∠AED=60°,则∠A的度数是( )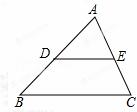
 0° D.70°
0° D.70° .
. .
.
 D.
D.