题目内容
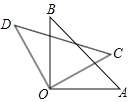
【题目】如图,将45°角三角板绕直角顶点旋转.
(1)问∠AOC与∠BOD大小关系,并说明理由;
(2)∠AOD与∠BOC的数量关系,并说明理由;
(3)若∠AOD=3∠BOC,求∠AOC的大小.
【答案】(1)∠AOC=∠BOD(2)∠AOD+∠BOC=180°;(3)45°.
【解析】
(1)由∠AOB-∠BOC=∠COD-∠BOC,即可得出结论;
(2)由角的关系容易得出结论;
(3)求出∠BOC=45°,即可得出∠AOC的度数.
(1)∠AOC=∠BOD;理由如下:
∵∠AOB=∠COD=90°,
∴∠AOB-∠BOC=∠COD-∠BOC,
即∠AOC=∠BOD;
(2)∠AOD+∠BOC=180°;理由如下:
∵∠AOB=∠COD=90°,
∴∠AOD+∠BOC=∠AOB+∠BOD+∠BOC=∠AOB+∠COD=90°+90°=180°;
(3)∵∠AOD=3∠BOC,∠AOD+∠BOC=180°,
∴∠BOC=45°,
∵∠AOB=90°,
∴∠AOC=45°.

练习册系列答案
相关题目
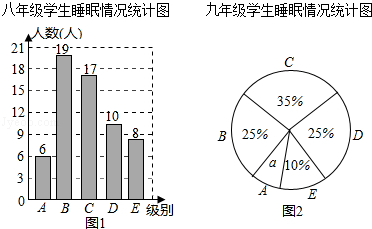
【题目】为了解某校八、九年级部分学生的睡眠情况,随机抽取了该校八、九年级部分学生进行调查,已知抽取的八年级与九年级的学生人数相同,利用抽样所得的数据绘制如图的统计图表:
睡眠情况分段情况如下
组别 | 睡眠时间x(小时) |
A | 4.5≤x<5.5 |
B | 5.5≤x<6.5 |
C | 6.5≤x<7.5 |
D | 7.5≤x<8.5 |
E | 8.5≤x<9.5 |
根据图表提供的信息,回答下列问题:
(Ⅰ)直接写出统计图中a的值 ![]()
(Ⅱ)睡眠时间少于6.5小时为严重睡眠不足,则从该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性分别有多大?