题目内容
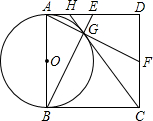 在正方形ABCD中,E为AD中点,AF丄BE交BE于G,交CD于F,连CG延长交AD于H.下列结论:
在正方形ABCD中,E为AD中点,AF丄BE交BE于G,交CD于F,连CG延长交AD于H.下列结论:
①CG=CB;②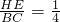 ;③
;③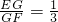 ;④以AB为直径的圆与CH相切于点G,其中正确的是________.
;④以AB为直径的圆与CH相切于点G,其中正确的是________.
①②③④
分析:连接OG、OC,构建全等三角形△BOC≌△GOC,然后由全等三角形的对应角相等推知∠OBC=∠OGC=90°,即OG⊥CH,故④正确;利用④中切线的性质可以推知①正确;由平行线截线段成比例可以证得②正确;最后由正方形的性质及勾股定理可以求得④正确.
解答: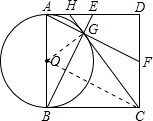 解:连接OG、OC.
解:连接OG、OC.
∵AF丄BE,
∴∠ABE=∠DAF;
在Rt△ABE和Rt△DAF中,
∵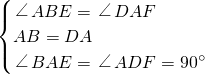 ,
,
∴Rt△ABE≌Rt△DAF(ASA),
∴AE=DF(全等三角形的对应边相等);
又∵E为AD中点,
∴F为DC的中点;
∵O为AB的中点,
∴OC∥AF,
∴OC⊥BE,
∴∠BOC=∠GOC;
在△BOC和△GOC中,
∵ ,
,
∴△BOC≌△GOC,
∴∠OBC=∠OGC=90°,即OG⊥CH,
∴以AB为直径的圆与CH相切于点G;
故④正确;
∵以AB为直径的圆与CH相切于点G,AB⊥BC,
∴CG=CB;
故①正确;
∵AD∥BC,
∴ =
=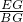 =
=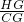 ;
;
∵CG=CB,
∴HG=HE;
又∵E为AD中点,
∴AH=HE=HG,即点H为AE的中点,
∴ =
=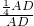 =
= ;
;
故②正确;
∵点F是CD的中点,
∴DF= AD;
AD;
∴AF= AD(勾股定理);
AD(勾股定理);
∵tan∠DAF= =
=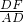 =
= ,
,
∴AG=2EG,
∴AE= EG=
EG= AD,
AD,
∴EG=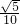 AD,
AD,
∴AG= AD,
AD,
∴FG=AF-AG= AD,
AD,
∴ =
= ;
;
故③正确;
综上所述,正确的说法有:①②③④.
故答案是:①②③④.
点评:本题综合考查了切线的性质与判定、全等三角形的判定与性质、正方形的性质等知识点.解答③选项时,也可以利用相似三角形的判定与性质.
分析:连接OG、OC,构建全等三角形△BOC≌△GOC,然后由全等三角形的对应角相等推知∠OBC=∠OGC=90°,即OG⊥CH,故④正确;利用④中切线的性质可以推知①正确;由平行线截线段成比例可以证得②正确;最后由正方形的性质及勾股定理可以求得④正确.
解答:
 解:连接OG、OC.
解:连接OG、OC.∵AF丄BE,
∴∠ABE=∠DAF;
在Rt△ABE和Rt△DAF中,
∵
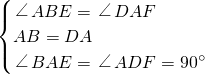 ,
,∴Rt△ABE≌Rt△DAF(ASA),
∴AE=DF(全等三角形的对应边相等);
又∵E为AD中点,
∴F为DC的中点;
∵O为AB的中点,
∴OC∥AF,
∴OC⊥BE,
∴∠BOC=∠GOC;
在△BOC和△GOC中,
∵
 ,
,∴△BOC≌△GOC,
∴∠OBC=∠OGC=90°,即OG⊥CH,
∴以AB为直径的圆与CH相切于点G;
故④正确;
∵以AB为直径的圆与CH相切于点G,AB⊥BC,
∴CG=CB;
故①正确;
∵AD∥BC,
∴
 =
=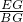 =
=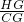 ;
;∵CG=CB,
∴HG=HE;
又∵E为AD中点,
∴AH=HE=HG,即点H为AE的中点,
∴
 =
=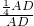 =
= ;
;故②正确;
∵点F是CD的中点,
∴DF=
 AD;
AD;∴AF=
 AD(勾股定理);
AD(勾股定理);∵tan∠DAF=
 =
=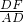 =
= ,
,∴AG=2EG,
∴AE=
 EG=
EG= AD,
AD,∴EG=
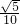 AD,
AD,∴AG=
 AD,
AD,∴FG=AF-AG=
 AD,
AD,∴
 =
= ;
;故③正确;
综上所述,正确的说法有:①②③④.
故答案是:①②③④.
点评:本题综合考查了切线的性质与判定、全等三角形的判定与性质、正方形的性质等知识点.解答③选项时,也可以利用相似三角形的判定与性质.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 已知:如图所示,在正方形ABCD中,E为AD的中点,F为DC上的一点,且DF=
已知:如图所示,在正方形ABCD中,E为AD的中点,F为DC上的一点,且DF= 18、在正方形ABCD中,点G是BC上任意一点,连接AG,过B,D两点分别作BE⊥AG,DF⊥AG,垂足分别为E,F两点,求证:△ADF≌△BAE.
18、在正方形ABCD中,点G是BC上任意一点,连接AG,过B,D两点分别作BE⊥AG,DF⊥AG,垂足分别为E,F两点,求证:△ADF≌△BAE.
 如图,在正方形ABCD中,P是CD上一点,且AP=BC+CP,Q为CD中点,求证:∠BAP=2∠QAD.
如图,在正方形ABCD中,P是CD上一点,且AP=BC+CP,Q为CD中点,求证:∠BAP=2∠QAD.