题目内容
设y=|x-1|+|x+1|，则下面四个结论中正确的是
- A.y没有最小值
- B.只有一个x使y取最小值
- C.有限个x（不止一个）y取最小值
- D.有无穷多个x使y取最小值
D
分析：根据非负数的性质，分别讨论x的取值范围，再判断y的最值问题．
解答：由题意得：当x＜-1时，y=-x+1-1-x=-2x；
当-1＜x＜1时，y=-x+1+1+x=2；
当x＞1时，y=x-1+1+x=2x；
故由上得当-1＜x＜1时，y有最小值为2；
故选D．
点评：本题主要考查利用非负数的性质求代数式的最值问题，注意按未知数的取值分情况讨论．
分析：根据非负数的性质，分别讨论x的取值范围，再判断y的最值问题．
解答：由题意得：当x＜-1时，y=-x+1-1-x=-2x；
当-1＜x＜1时，y=-x+1+1+x=2；
当x＞1时，y=x-1+1+x=2x；
故由上得当-1＜x＜1时，y有最小值为2；
故选D．
点评：本题主要考查利用非负数的性质求代数式的最值问题，注意按未知数的取值分情况讨论．
练习册系列答案
相关题目
八年级某班级部分同学去植树，若每人平均植树7棵，还剩9棵，若每人平均植树9棵，则有1名同学植树的棵数不到8棵．若设同学人数为x人，下列各项能准确的求出同学人数与种植的树木的数量的是（ ）
| A、7x+9-9（x-1）＞0 | |||||
| B、7x+9-9（x-1）＜8 | |||||
C、
| |||||
D、
|
已知⊙O1的半径为R，周长为C．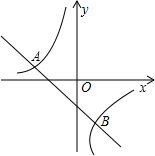
如图，若反比例函数y=-