题目内容
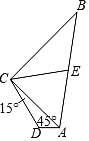
【题目】已知四边形ABCD中,AB=10,BC=8,CD=![]() ∠DAC=45°,∠DCA=15°.
∠DAC=45°,∠DCA=15°.
(1)求△ADC的面积;
(2)若E为AB的中点,求线段CE的长。
【答案】(1)![]() ;(2)CE=5.
;(2)CE=5.
【解析】
(1)过点C作CF⊥AD,交AD延长线于点F,构造含有30度角的直角△CFD,通过解该直角三角形求得DF、CF的长度,进而利用等腰直角△ACF的性质求得AD的长度,结合三角形的面积公式解答即可;
(2)由勾股定理的逆定理得到△ABC是直角三角形,由“直角三角形斜边上的中线等于斜边的一半”解答.
(1)过点C作CF⊥AD,交AD延长线于点F,
∵∠DAC=45°,∠DCA=15°,
∴∠CDF=∠DAC+∠DCA=45°+15°=60°,
在Rt△CFD中,CD=2![]() ,
,
∴DF=![]() CD=
CD=![]() ,CF=
,CF=![]() ,
,
∴AD=AFDF=3![]() ,
,
∴S△ADC=![]() AD×CF=
AD×CF=![]() ×(2
×(2![]()
![]() )×3
)×3![]() =93
=93![]() .
.
(2)在Rt△AFC中,∵∠DAC=45°,CF=3![]() ,
,
∴AC=![]() CF=
CF=![]() ×3
×3![]() =6,
=6,
在△ABC中,∵AC2+BC2=62+82=AB2
∴△ABC是直角三角形,
又∵E为AB中点,
∴CE=![]() AB=
AB=![]() ×10=5.
×10=5.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目