Question

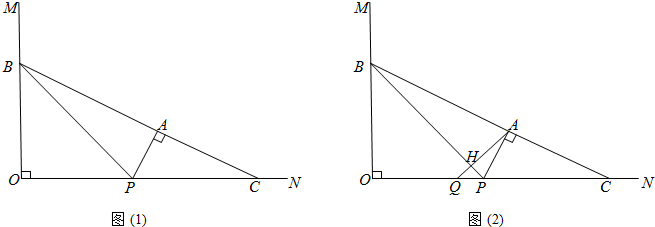
（2013•奉贤区一模）如图（1），已知∠MON=90°，点P为射线ON上一点，且OP=4，B、C为射线OM和ON上的两个动点（OC＞OP），过点P作PA⊥BC，垂足为点A，且PA=2，连接BP．
（1）若

S△PAC

S四边形ABOP

=

1

2

时，求tan∠BPO的值；
（2）设PC=x，

AB

BC

=y，求y与x之间的函数解析式，并写出定义域；
（3）如图（2），过点A作BP的垂线，垂足为点H，交射线ON于点Q，点B、C在射线OM和ON上运动时，探索线段OQ的长是否发生变化？若不发生变化，求出它的值．若发生变化，试用含x的代数式表示OQ的长．

Answer 1

分析：（1）根据有两对角相等的三角形相似可证明△CAP∽△COB，由相似三角形的性质可知：

S△PAC

S△COB

=（

AP

OB

）²，在由已知条件可求出OB的长，由正切的定义计算即可；
（2）作AE⊥PC于E，易证△PAE∽△PCA，根据相似三角形的性质：对应边的比值相等PE=

4

x

，再利用平行线的性质即可得到

AB

BC

=

OE

OC

，所以y=

4+ 4 x

x+4

，整理即可得到求y与x之间的函数解析式，并写出定义域即可；
（3）点B、C在射线OM和ON上运动时，探索线段OQ的长不发生变化，由△PAH∽△PBA得：

PA

PB

=

PH

PA

，即PA²=PH•PB，由△PHQ∽△POB得：

PQ

PB

=

PH

PO

即PQ•PO=PH•PB，所以PA²=PQ•PO，再由已知数据即可求出OQ的长．

解答：解：（1）∵PA⊥BC，
∴∠CAP=90°
∴∠CAP=∠0=90°，
又∵∠ACP=∠OCB，
∴△CAP∽△COB，
∴

S△PAC

S△COB

=（

AP

OB

）²，
∵

S△PAC

S四边形ABOP

=

1

2

，
∴

S△PAC

S△COB

=

1

3

，
∴（

AP

OB

）²=

1

3

，
∵AP=2，
∴OB=2

3

，
在Rt△OBP中，tan∠OPB=

OB

OP

=

3

2

；
（2）作AE⊥PC于E，
∴∠AEP=∠CAP=90°
∵∠APE=∠CPA，
∴△PAE∽△PCA，
∴

PA

PC

=

PE

PA

，
∴2²=PE•x，
∴PE=

4

x

，
∵∠MON=∠AEC，
∴AE∥OM，
∴

AB

BC

=

OE

OC

，
∴y=

4+ 4 x

x+4

，
整理得：y=

4x+4

x2+4x

（x＞0）；
（3）点B、C在射线OM和ON上运动时，探索线段OQ的长不发生变化，
理由如下：由△PAH∽△PBA得：

PA

PB

=

PH

PA

，即PA²=PH•PB，
由△PHQ∽△POB得：

PQ

PB

=

PH

PO

即PQ•PO=PH•PB，
∴PA²=PQ•PO，
∵PA=2，PO=4，
∴PQ=1，
∴OQ=3，
即点B、C在射线OM和ON上运动时，线段OQ的长不发生变化，长度是3．

点评：本题考查了相似三角形的判定和性质、锐角三角函数的定义、平行线的判定和性质、由比例式引出的线段之间的函数关系，题目的综合性综合性很强，特别是第三问的动点问题是中考题中的难点．