题目内容
【题目】在
中，
，
，
于点
.
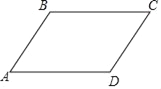
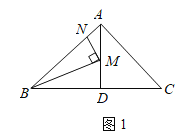
（1）如图1所示，点
分别在线段
上，且
，当
时，求线段
的长；
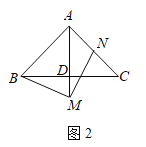
（2）如图2，点
在线段
的延长线上，点
在线段
上，（1）中其他条件不变.
①线段的长为 ；
②求线段
的长.
【答案】（1）
；（2）①
，②
【解析】
（1）根据等腰三角形的性质、直角三角形的性质得到
，求出∠MBD=30°，根据勾股定理计算即可；
（2）①方法同（1）求出AD和DM的长即可得到AM的长；
②过点
作
交
的延长线于点
，首先证明
得到BE=AN，再根据勾股定理求出AE的长，利用线段的和差关系可求出BE的长，从而可得AN的长.
解：（1）
，
，
，
，
，
，
，
在
中，
，
，
根据勾股定理，
，
，
，
，
，
，
，
在
中，
，
由勾股定理得，
，
即
，
解得，
，
；
（2）①方法同（1）可得
，，
∴AM=AD+DM=，
故答案为：；
②过点作交的延长线于点，如图，
，
，
，
，
，
，，
，
，
，
，
在
中，，
由①
，
.
根据勾股定理，
，
.
练习册系列答案
阅读快车系列答案
相关题目
