题目内容
 已知二次函数y=(x-1)2-4的图象如图所示.
已知二次函数y=(x-1)2-4的图象如图所示.
(1)求抛物线与x轴交点A、B的坐标(点A在点B的左侧),及与y轴的交点C的坐标;
(2)设抛物线的顶点为点D,求△BCD的面积S;
(3)在抛物线上是否存在点E,使以A、B、C、E为顶点的四边形是梯形?若存在,请求出点E的坐标,并说明理由;若不存在,请说明理由.
解:(1)0=(x-1)2-4,
解得x1=-1,x2=3,
∴A(-1,0)B(3,0),
当x=0时,y=-3,
∴C(0,-3);
(2)∵y=(x-1)2-4,
∴D(1,-4),
∴BC= ,BD=
,BD= ,CD=
,CD= ,
,
∴BC2+CD2=BD2,
∴∠BCD=90°,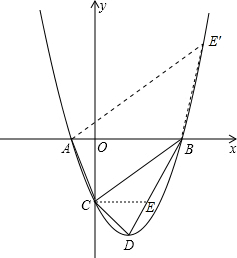
∴△BCD的面积S= ×
× ×
× =3;
=3;
(3)∵A、B、C、E为顶点的四边形是梯形,
∴①当AB∥CE时,
∴点E的纵坐标为-3,
∴-3=(x-1)2-4,
解得x1=2,x2=0,
∴点E的坐标为(2,-3).
②当AC∥BE时,
由B,C,的坐标可求直线BC的解析式为:y=x-3,
故直线AE的解析式为:y=x+b,
将A(-1,0)代入得出:y=x+1,
将两函数联立得出:x+1=(x-1)2-4,
解得:x1=-1,x2=4,
当x=4时y=5,
故E点坐标为:(4,5),
③当AE∥BC时,直线AC的解析式为:y=-3x-3,
直线BE的解析为:y=-3x+9,
将两函数联立得出:-3x+9=(x-1)2-4,
解得:x1=-4,x2=3,
当x=-4时y=21,
故E点坐标为:(-4,21),
综上所述:E点坐标为:(2,-3),(4,5),(-4,21).
分析:(1)y=0,即可求得抛物线与x轴的交点坐标;x=0,可求得抛物线与y轴的交点坐标;
(2)易得△BCD为直角三角形,根据三角形的面积公式即可求得△BCD的面积S;
(3)利用当AB∥CE时,②当AC∥BE时,③当AE∥BC时分别求出即可.
点评:用到的知识点为:抛物线与x轴的交点的纵坐标为0,与y轴交点的横坐标为0;平行与x轴的直线上的点的纵坐标相等.
解得x1=-1,x2=3,
∴A(-1,0)B(3,0),
当x=0时,y=-3,
∴C(0,-3);
(2)∵y=(x-1)2-4,
∴D(1,-4),
∴BC=
 ,BD=
,BD= ,CD=
,CD= ,
,∴BC2+CD2=BD2,
∴∠BCD=90°,

∴△BCD的面积S=
 ×
× ×
× =3;
=3;(3)∵A、B、C、E为顶点的四边形是梯形,
∴①当AB∥CE时,
∴点E的纵坐标为-3,
∴-3=(x-1)2-4,
解得x1=2,x2=0,
∴点E的坐标为(2,-3).
②当AC∥BE时,
由B,C,的坐标可求直线BC的解析式为:y=x-3,
故直线AE的解析式为:y=x+b,
将A(-1,0)代入得出:y=x+1,
将两函数联立得出:x+1=(x-1)2-4,
解得:x1=-1,x2=4,
当x=4时y=5,
故E点坐标为:(4,5),
③当AE∥BC时,直线AC的解析式为:y=-3x-3,
直线BE的解析为:y=-3x+9,
将两函数联立得出:-3x+9=(x-1)2-4,
解得:x1=-4,x2=3,
当x=-4时y=21,
故E点坐标为:(-4,21),
综上所述:E点坐标为:(2,-3),(4,5),(-4,21).
分析:(1)y=0,即可求得抛物线与x轴的交点坐标;x=0,可求得抛物线与y轴的交点坐标;
(2)易得△BCD为直角三角形,根据三角形的面积公式即可求得△BCD的面积S;
(3)利用当AB∥CE时,②当AC∥BE时,③当AE∥BC时分别求出即可.
点评:用到的知识点为:抛物线与x轴的交点的纵坐标为0,与y轴交点的横坐标为0;平行与x轴的直线上的点的纵坐标相等.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
已知二次函数y=-x2+bx+c的图象过点A(1,2),B(3,2),C(0,-1),D(2,3).点P(x1,y1),Q(x2,y2)也在该函数的图象上,当0<x1<1,2<x2<3时,y1与y2的大小关系正确的是( )
| A、y1≥y2 | B、y1>y2 | C、y1<y2 | D、y1≤y2 |
 (2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
(2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;