题目内容
【题目】定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
理解:
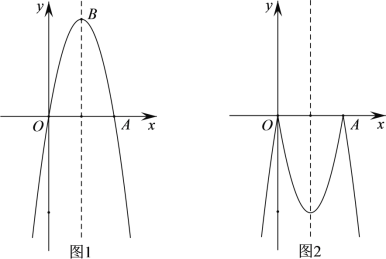
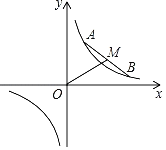
![]() 如图1,点
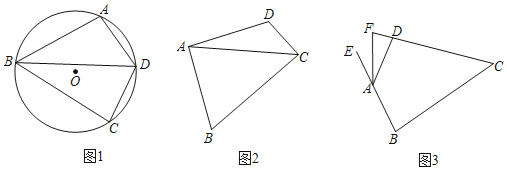
如图1,点![]() 在
在![]() 上,
上,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,连接
,连接![]() 求证:四边形
求证:四边形![]() 是等补四边形;
是等补四边形;
探究:
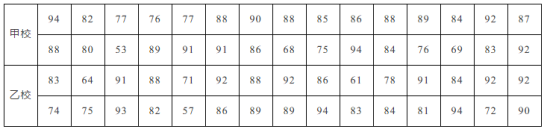
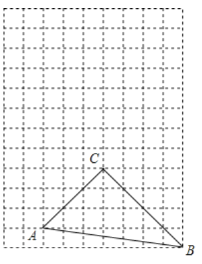
![]() 如图2,在等补四边形
如图2,在等补四边形![]() 中
中![]() 连接
连接![]() 是否平分
是否平分![]() 请说明理由.
请说明理由.
运用:
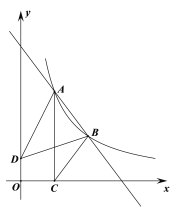
![]() 如图3,在等补四边形
如图3,在等补四边形![]() 中,
中,![]() ,其外角
,其外角![]() 的平分线交
的平分线交![]() 的延长线于点
的延长线于点![]() 求
求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() 平分
平分![]() ,理由见解析;(3)
,理由见解析;(3)![]() .
.
【解析】
![]() 由圆内接四边形互补可知
由圆内接四边形互补可知![]() ,再证
,再证![]() ,即可根据等补四边形的定义得出结论;
,即可根据等补四边形的定义得出结论;
![]() 过点
过点![]() 分别作
分别作![]() 于点
于点![]() ,
,![]() 垂直
垂直![]() 的延长线于点
的延长线于点![]() ,证
,证![]() ,得到
,得到![]() ,根据角平分线的判定可得出结论;
,根据角平分线的判定可得出结论;
![]() 连接
连接![]() ,先证
,先证![]() 推出
推出![]() 再证
再证![]() 利用相似三角形对应边的比相等可求出
利用相似三角形对应边的比相等可求出![]() 的长.
的长.
![]() 证明:
证明:![]() 四边形
四边形![]() 为圆内接四边形,
为圆内接四边形,
![]()
![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 是等补四边形;
是等补四边形;

![]()
![]() 平分
平分![]() ,理由如下:
,理由如下:
如图2,过点![]() 分别作
分别作![]() 于点
于点![]() ,
,![]() 垂直
垂直![]() 的延长线于点
的延长线于点![]() ,则
,则![]() ,
,

![]() 四边形
四边形![]() 是等补四边形,
是等补四边形,
![]()
又![]()
![]()
![]()
![]()
![]()
![]() 是
是![]() 的平分线,即
的平分线,即![]() 平分
平分![]()
![]() 如图3,连接
如图3,连接![]() ,
,

![]() 四边形
四边形![]() 是等补四边形,
是等补四边形,
![]()
又![]() ,
,
![]()
![]() 平分
平分![]()
![]()
由![]() 知,
知,![]() 平分
平分![]()
![]()
![]()
又![]()
![]()
![]()
即![]()
![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】水果基地为了选出适应市场需求的小西红柿秧苗,在条件基本相同的情况下,把两个品种的小西红柿秧苗各300株分别种植在甲、乙两个大棚.对市场最为关注的产量和产量的稳定性进行了抽样调査,过程如下,请补充完整.
收集数据 从甲、乙两个大棚各收集了25株秧苗上的小西红柿的个数:
甲 26 32 40 51 44 74 44 63 73 74 81 54 62
41 33 54 43 34 51 63 64 73 64 54 33
乙 27 35 46 55 48 36 47 68 82 48 57 66 75
27 36 57 57 66 58 61 71 38 47 46 71
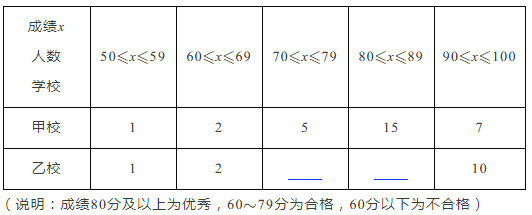
整理数据 按如下分组整理、描述这两组样本数据:

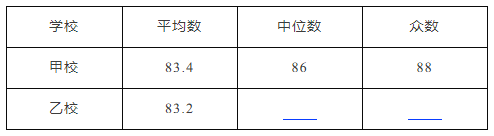
(说明:45个以下为产量不合格,45个及以上为产量合格,其中45~65个为产量良好,65~85个为产量优秀)分析数据 组样本数据的平均数、众数和方差如下表所示:
大棚 | 平均数 | 众数 | 方差 |
甲 | 53 | 54 | 236.24 |
乙 | 53 | 57 | 215.04 |
得出结论 a.估计甲大棚产量良好的秧苗数为________株;b.可以推断出________大棚的小西红柿秧苗品种更适应市场需求,理由为________________.(至少从两个不同的角度说明推断的合理性)