题目内容
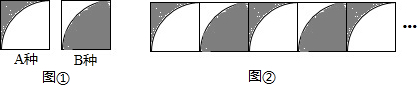
边长为2的两种正方形卡片如图①所示，卡片中的扇形半径均为2．图②是交替摆放A、B两种卡片得到的图案．若摆放这个图案共用两种卡片21张，则这个图案中阴影部分图形的面积和为 （结果保留π）．
【答案】分析：首先求得A，B两种卡片阴影部分的面积，然后确定21张卡片中A，B各自的张数，即可求解．
解答：解：A种的面积是：4-
π×22=4-π；
B种的面积是：
π×22=π．
两种卡片21张，则有A种11张，B中10张，因而面积的和是：11（4-π）+10π=44-π．
故答案是：44-π．
点评：本题主要考查了扇形面积的计算，正确确定21张卡片中A，B各自的张数是解题的关键．
解答：解：A种的面积是：4-
π×22=4-π；B种的面积是：
π×22=π．两种卡片21张，则有A种11张，B中10张，因而面积的和是：11（4-π）+10π=44-π．
故答案是：44-π．
点评：本题主要考查了扇形面积的计算，正确确定21张卡片中A，B各自的张数是解题的关键．
练习册系列答案
相关题目
